

下一頁: H
上一頁: 三、選填題
前一頁: F
坐標平面上有一質點沿方向
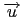 = (1, 2)
前進。現欲在此平面上置一直線 L,使得此質點碰到 L
時依光學原理(入射角等於反射角)反射,之後沿方向
= (1, 2)
前進。現欲在此平面上置一直線 L,使得此質點碰到 L
時依光學原理(入射角等於反射角)反射,之後沿方向
 = (- 2, 1) 前進,則直線 L 的方向向量應為
= (- 2, 1) 前進,則直線 L 的方向向量應為
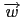 = (1,?)。
= (1,?)。
說明:這一題出題者問的是坐標面上要如何擺置一直線方能使一行進的質點在碰到此直線後會沿著特定方向反射.
較特別的是, 一般在坐標平面上我們較習慣用斜率來表達一直線,
此題中卻要求用方向向量. 或許出題者就是要檢測同學這之間的轉換,
也可能是為了引導同學用向量來處理. 確實此題用基本的向量性質就可處理.
不過對向量不熟悉的同學,
亦可將這些向量具體的擺在坐標平面上用較熟悉的坐標處理,
只是程序上較麻煩.
首先用坐標幾何的方法處理此題需先了解, 這個問題只關係到``方向'',
和位置是無關的. 所以我們可假定這個質點碰到直線的位置是
(0, 0). 因為質點是依 (1, 2) 這個方向跑,
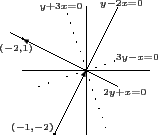
所以我們知這個質點會沿著通過 (0, 0) 點且斜率為 2 的直線 (即
y - 2x = 0) 前進. 當質點在 (0, 0) 點反射後其前進方向為 (- 2, 1),
故得這個質點反射後是依 2y + x = 0 這條直線前進. 也就是說 y - 2x = 0
是入射直線, 而 2y + x = 0 是反射直線, 因此依入射角等於反射角原則,
我們知所求直線應為此二直線的一個角平分線. 利用角平分線的性質得到,
y - 2x = 0 和 2y + x = 0 的角平分線應為
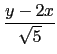
= ±
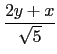
,
也就是 y + 3x = 0 和 3y - x = 0 這兩條直線.
現在我們的問題是, 到底應是哪條線呢? 注意, 由於我們假設入射的向量會在
(0, 0) 點碰到直線而反射所以若要將入射向量 (1, 2) 擺在坐標平面上,
應將始點置於 (- 1, - 2) 這樣終點才會是 (0, 0) (也就是說質點是由
(- 1, - 2) 跑到 (0, 0) 再反射. 而反射向量 (- 2, 1) 就應是始點為
(0, 0) 而終點為 (- 2, 1) (也就是說質點在 (0, 0) 點反射後, 會往
(- 2, 1) 這一點跑). 所以 (- 1, - 2) 和 (- 2, 1)
會在我們要求的直線的同側. 因為將 x = - 1, y = - 2 和 x = - 2, y = 1 代入,
y + 3x 會同號而代入 3y - x 會異號, 所以 y + 3x = 0 是我們要求的直線.
故由其斜率為 -3 知其方向向量為 (1, - 3).
當然了我們也可直接畫圖來判斷出此直線斜率應為 -3, 如下圖.
此題若用向量來解就簡單多了, 我們用以下略圖稍作解釋.
由於入射角等於反射角, 當
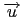 和
和
 長度相等時, 它們在 L
上的投影向量方向與長度都相同 (即投影向量相等). 因此知
長度相等時, 它們在 L
上的投影向量方向與長度都相同 (即投影向量相等). 因此知
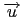 和
和
 分別對
分別對
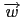 作內積其值會相等 (即
作內積其值會相等 (即
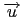 .
. 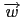 =
=  .
. 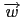 ).
此題由於
).
此題由於
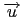 = (1, 2) 且
= (1, 2) 且
 = (- 2, 1),
它們的長度皆為
= (- 2, 1),
它們的長度皆為 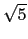 . 所以若 w = (1, c), 則由
. 所以若 w = (1, c), 則由
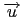 .
. 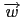 =
=  .
. 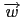 , 可得 1 + 2c = - 2 + c. 因此知 c = - 3.
, 可得 1 + 2c = - 2 + c. 因此知 c = - 3.
對於內積不熟悉的同學, 也可由向量加法的定義方式處理本題.
在向量加法定義中我們有所謂的「三角形法」, 也就是說要得到向量
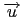 和
和
 之和, 我們可將
之和, 我們可將
 的始點置於
的始點置於
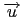 之終點上,
這樣一來以
之終點上,
這樣一來以
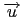 +
+  這個向量就是始點為
這個向量就是始點為
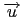 之始點而終點為
之始點而終點為
 之終點的向量. 如下圖, 若
之終點的向量. 如下圖, 若
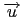 的始點為 A 終點為 B, 則將
的始點為 A 終點為 B, 則將
 的始點置於 B
上. 此時若
的始點置於 B
上. 此時若
 的終點為 C, 則
的終點為 C, 則
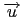 +
+  =
= 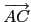 .
.
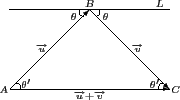
特別地, 當
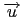 和
和
 長度相等時,
三角形 ABC 是一個以
長度相等時,
三角形 ABC 是一個以
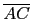 為底的等腰三角形. 因此若假設入射角為
為底的等腰三角形. 因此若假設入射角為
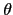 (此時反射角亦為
(此時反射角亦為 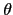 ) 且假設
) 且假設
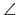 BAC =
BAC = 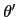 (此時
(此時
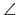 ACB =
ACB = 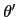 ), 則由於
2
), 則由於
2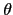 +
+ 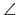 ABC = 180o = 2
ABC = 180o = 2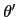 +
+ 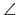 ABC, 可得
ABC, 可得
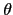 =
= 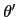 . 亦即
. 亦即
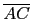 會和 L 平行, 也就是說
會和 L 平行, 也就是說
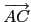 就是 L 的
方向向量. 因此由
就是 L 的
方向向量. 因此由
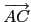 =
= 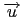 +
+  = (1, 2) + (- 2, 1) = (- 1, 3),
可知 (1, - 3) (因為向量 (1, - 3) 和 (- 1, 3) 平行) 是 L
的方向向量.
當然了若同學習慣用「平行四邊形法」來處理向量的加法一樣可以解釋.
首先將
= (1, 2) + (- 2, 1) = (- 1, 3),
可知 (1, - 3) (因為向量 (1, - 3) 和 (- 1, 3) 平行) 是 L
的方向向量.
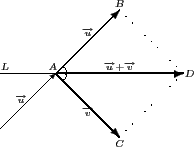
當然了若同學習慣用「平行四邊形法」來處理向量的加法一樣可以解釋.
首先將
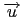 和
和
 的始點置於同一點
A 如下圖, 則利用
的始點置於同一點
A 如下圖, 則利用
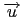 和
和
 的終點 B 和 C, 我們可得一平行四邊形 ABDC. 此時
的終點 B 和 C, 我們可得一平行四邊形 ABDC. 此時
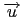 +
+  =
= 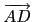 .
.
特別地, 當
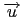 和
和
 長度相等時,
三角形 ABD 和三角形 ACD 全等, 也就是說
長度相等時,
三角形 ABD 和三角形 ACD 全等, 也就是說
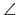 BAD =
BAD = 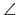 CAD.
因此得
CAD.
因此得
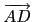 =
= 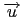 +
+  為 L 的方向向量.
為 L 的方向向量.
要注意, 雖然上面所提向量的方法需要
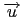 和
和
 的長度相等. 不過若題目所給的向量長度不同,
我們也可將其中的一個向量伸縮使其和另一向量長度相等,
然後再用上述方法處理.
的長度相等. 不過若題目所給的向量長度不同,
我們也可將其中的一個向量伸縮使其和另一向量長度相等,
然後再用上述方法處理.


下一頁: H
上一頁: 三、選填題
前一頁: F
Li
2008-03-06
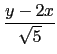 = ±
= ±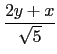 ,
,
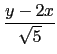 = ±
= ±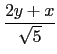 ,
,

![]() 和
和
![]() 之和, 我們可將
之和, 我們可將
![]() 的始點置於
的始點置於
![]() 之終點上,
這樣一來以
之終點上,
這樣一來以
![]() +
+ ![]() 這個向量就是始點為
這個向量就是始點為
![]() 之始點而終點為
之始點而終點為
![]() 之終點的向量. 如下圖, 若
之終點的向量. 如下圖, 若
![]() 的始點為 A 終點為 B, 則將
的始點為 A 終點為 B, 則將
![]() 的始點置於 B
上. 此時若
的始點置於 B
上. 此時若
![]() 的終點為 C, 則
的終點為 C, 則
![]() +
+ ![]() =
= ![]() .
.
![]() 和
和
![]() 的長度相等. 不過若題目所給的向量長度不同,
我們也可將其中的一個向量伸縮使其和另一向量長度相等,
然後再用上述方法處理.
的長度相等. 不過若題目所給的向量長度不同,
我們也可將其中的一個向量伸縮使其和另一向量長度相等,
然後再用上述方法處理.