H

已知坐標平面上圓 O₁ : (x - 7)² + (y - 1)² = 144 與 O₂ : (x + 2)² + (y - 13)² = 9 相切，且此兩圓均與直線 L : x = - 5 相切。若 $\Gamma$ 為以 L 為準線的拋物線，且同時通過 O₁ 與 O₂ 的圓心，則 $\Gamma$ 的焦點坐標為何？（化為最簡分數）

說明:這一題是給定兩點 P, Q 和一直線 L 求過 P, Q 且以 L 為準線的拋物線. 題目中多給了兩個圓的訊息, 很明顯的出題者是希望同學利用拋物線的定義解題. 然而因為準線是鉛直線, 此拋物線是標準型的拋物線, 所以若直接用拋物線方程式來解亦可, 不過就比較繁雜了.

由於準線 L : x = - 5 是一鉛直線, 若此拋物線頂點為 (a, b) 且焦距為 c, 則我們有此拋物線方程式為 (y - b)² = 4c(x - a). 若能利用題目給的訊息解出 a, b, c, 就能求得焦點坐標了. 首先 (a, b) 為頂點, L 為準線, 所以焦距 c 就是 (a, b) 到直線 x = - 5 的距離, 因此得 c = $\left\vert\vphantom{ a+5}\right.$a + 5$\left.\vphantom{ a+5}\right\vert$. 然而拋物線上的點都應在準線 x = - 5 的同側, 又已知拋物線通過 O₁, O₂ 的圓心 P(7, 1), Q(- 2, 13) 故知拋物線應在直線 x = - 5 的右側, 故知 a > - 5, 而得 c = a + 5. 再一次利用拋物線通過 O₁, O₂ 的圓心 P(7, 1), Q(- 2, 13), 我們知 x = 7, y = 1 和 x = - 2, y = 13 需滿足拋物線方程式, 因此我們可得以下有關 a, b 的聯立方程式

$$\left\{\vphantom{ \begin{array}{rcl} (1-b)^2 & = & 4(a+5)(7-a) \\ (13-b)^2 & = & 4(a+5)(-2-a) \\ \end{array}%% }\right.$$$$\begin{array}{rcl} (1-b)^2 & = & 4(a+5)(7-a) \\ (13-b)^2 & = & 4(a+5)(-2-a) \\ \end{array}$$.

先將兩式相減得 3a - 2b + 29 = 0, 再將 b = (3a + 29)/2 代回第一式化簡得 25a² + 130a + 169 = 0, 也就是 (5a + 13)² = 0. 因此得 a = - 13/5 且 b = 53/5, 再由 c = a + 5 得 c = 12/5. 也就是說此拋物線的頂點為 (- 13/5, 53/5) 且焦距為 12/5. 故由準線是鉛直線 (x = - 5) 知貫軸為水平線 y = 53/5, 再因焦點在貫軸上且和頂點距離為 c, 得焦點坐標為 (- 1/5, 53/5).

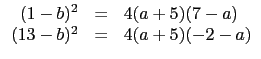上面這個方法可以看出來計算頗複雜, 而且題目若給的準線不是鉛直線或水平線, 不懂坐標轉換的同學幾乎就無計可施. 一般來說這樣的問題我們會用拋物線的定義處理. 依拋物線的定義, 拋物線上一點到準線的距離等於這一點到焦點的距離. 因此若我們以此點作圓心畫一圓使其和準線相切, 那麼這個圓的半徑就是此點到準線的距離, 因此焦點就會落在圓周上. 現在若又知這個拋物線通過另一點, 我們就依樣畫葫蘆, 以此點為圓心畫一與準線相切的圓. 如此一來焦點都會在畫出的這兩個圓的圓周上, 所以會落在這兩圓的交點上. 此題題目已知拋物線通過 O₁, O₂ 的圓心且準線皆和 O₁, O₂ 相切, 所以出題者已好心將這兩個圓畫好給我們了. 我們只要求出這兩圓的交點即可, 也就是說我們只要解聯立方程式

$$\left\{\vphantom{ \begin{array}{rcl} (x-7)^2+(y-1)^2&=&144 \\ (x+2)^2+(y-13)^2&=&9 \\ \end{array}%% }\right.$$$$\begin{array}{rcl} (x-7)^2+(y-1)^2&=&144 \\ (x+2)^2+(y-13)^2&=&9 \\ \end{array}$$

即可. 當然我們還可利用題目給的另外的訊息, 就是 ``O₁ 與 O₂ 相切'' 而知交點就是在 O₁ 與 O₂ 的切點上. 因此交點會在 O₁, O₂ 連線上, 且因為交點距離 O₁, O₂ 的圓心分別就是 O₁, O₂ 的半徑 12, 3, 故由分點公式得焦點坐標為

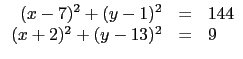
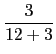$${\frac{3}{12+3}}$$(7, 1) + 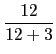$${\frac{12}{12+3}}$$(- 2, 13) = ($${\frac{-1}{5}}$$,$${\textstyle\frac{53}{5}}$$).

最後我們說明一下, 一般來說給定兩點 P, Q 和一直線 L, 並不一定會有唯一的拋物線會以 L 為準線且過 P, Q 兩點. 這完全要看分別以 P, Q 為圓心, P, Q 到 L 的距離 r₁, r₂ 為半徑的兩個圓相交的情形. 也就是說若 P, Q 的距離大於兩圓半徑之和 (即 $\overline{PQ}$ > r₁ + r₂), 則兩圓不相交, 故知無此拋物線; 若 P, Q 的距離小於兩圓半徑之和 (即 $\overline{PQ}$ < r₁ + r₂), 則兩圓交於兩點, 表示這兩點皆有可能為拋物線之焦點, 故知會有兩個拋物線以 L 為準線且過 P, Q 兩點; 然而如本題, P, Q 的距離等於兩圓半徑之和 (即 $\overline{PQ}$ = r₁ + r₂), 此時兩圓切於一點, 故僅會有一個拋物線以 L 為準線且過 P, Q 兩點.