(1) 每班至少會有一人被抽中
(2) 抽出來的男生人數一定比女生人數多
(3) 已知小文是男生,小美是女生,則小文被抽中的機率大於小美被抽中的機率
(4) 若學生甲和學生乙在同一班,學生丙在另外一班,則甲、乙兩人同時被抽中的機
率跟甲、 丙兩人同時被抽中的機率一樣
(5) 學生A和學生B是兄弟,他們同時被抽中的機率小於
![]() .
.
說明:本題是檢測同學是否清楚所謂「隨機」的概念.
隨機抽樣雖然高中數學各版本都有提及,
不過基於「隨機」的概念不容易描述,
幾乎沒有一個版本能將隨機抽樣定義清楚.
同學們對於隨機這個概念可能都是憑``感受''處理,
本題確實可檢測出同學們對隨機這個概念的感受是否正確,
不過在課本都無明確定義之情況下, 要正確無誤的答對選項實屬不易.
基本上在 800 人中隨機抽樣抽出 80人, 表示這 800 人中任意 80 人的組合都有可能會發生且其發生的機會都相等. 基於所有可能的組合都會發生所以有可能抽出的 80 人剛好是某兩班的全體同學(有可能會發生只是機率很低而已); 也有可能抽出的都是女生. 因此選項 (1), (2) 都是錯的. 另外基於所有可能的組合發生的機會都相等, 所以很容易理解每個人會被抽中的機率都相等(不分男女)且任兩個人被抽中的機率也都相等(不分班別). 因此選項 (3) 是錯的而選項 (4) 是對的. 或許有許多同學認為男生人數比較多, 被抽中的機率當然比較大, 而無法理解為何選項 (3) 不對. 沒錯! 男生被抽中的機率是比較大, 但是題目是要抽中特定的男生小文, 所以在比較多的男生中抽出小文的機率相對於比在女生中抽出小美的機率小. 因此和前面所提抽中男生的機率比抽中女生的機率大, 兩相平衡是會造成小文和小美被抽中的機率相等.
最後一個選項是屬於機率問題, 要計算同時抽中 A,B 兩人的機率.
既然是隨機抽樣, 每一個樣本點被抽出的機率相同,
我們可用古典機率的方法求此機率. 也就是先算出從 800 人中選取 80
人的所有組合數 (即
800![]() ) 再除掉從這 800 人選取的 80
人中包含 A,B 二人的所有組合數 (由於 80 人中需包含 A,B 二人,
這相當於從 798 人中選取 78 人, 即
798
) 再除掉從這 800 人選取的 80
人中包含 A,B 二人的所有組合數 (由於 80 人中需包含 A,B 二人,
這相當於從 798 人中選取 78 人, 即
798![]() ). 故得此機率為
). 故得此機率為
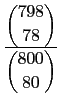 =
= 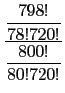 =
= 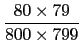 <
<