

下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: A
若三角形 ABC 的
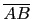 = 8 、
= 8 、
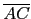 = 4
= 4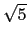 及
cos
及
cos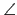 BAC = 1/
BAC = 1/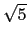 ,則
sin
,則
sin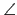 ACB =?
ACB =?
說明:本題是一般基礎的三角問題. 已知ㄧ三角形的兩邊長及其夾角 (即 SAS),
要求出其他的邊和角.
只要懂得適時運用餘弦定理或正弦定理就能處理這一題.
本題雖不難,
不過我們想利用這個機會討論一下如何由三角形的幾個邊角關係來確認一個三角形.
所謂確認一個三角形意思就是說能確定此三角形的三邊長和三個角.
一般只要用正弦及餘弦定理就能處理此類問題,
所以這也讓同學了解這兩個定理的適用時機.
以下我們將用一般習慣的符號設定. 我們直接用 A, B, C 表示三角形 ABC
三個內角的角度, 而分別用 a, b, c 表式角 A, B, C 的對邊 (即
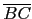 ,
,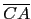 ,
,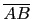 ) 的邊長, 如下圖所示.
) 的邊長, 如下圖所示.
首先我們複習一下正弦和餘弦定理.
正弦定理:
餘弦定理:
| a2 |
= |
b2 + c2 - 2bc cos A |
|
| b2 |
= |
a2 + c2 - 2ac cos B |
|
| c2 |
= |
a2 + b2 - 2ab cos C |
|
這裡可以看出只要是三邊長和三內角即
a, b, c, A, B, C 中有三個值已知,
應該就可以代入正弦或餘弦定理的等式中, 而求出其他的值.
不過在使用正弦定理要注意, 有可能得到的是一個比值而不是正確的數值.
另外要注意求出
sin A, sin B 或 sin C 之值並不表示確定 A, B 或
C 的值為何. 這是因為 sin x 在
0o < x < 180o
中並不是一對一的 (因
sin(180o - x) = sin x).
這些我們在下面會再說明. 在此可以知道在談用邊角關係確認一個三角形,
至少需假設已知其中三個值.
事實上可以用邊角關係確定唯一的三角形有以下三種情形.
即知道三邊長 a, b, c 之值. 此時我們可用餘弦定理求出
cos A, cos B
及 cos C 之值. 由於 cos x 在
0o < x < 180o
中是一對一的, 這表示我們確定了 A, B, C 之值.
當然了我們也可以用正弦定理, 不過此時我們僅得到
sin A : sin B : sin C = a : b : c 這個比值, 而不是
sin A, sin B, sin C 之值. 此時即使利用
A + B + C = 180o 可得
sin(A + B) = sin C, 再利用和角公式求出
sin A, sin B, sin C 之值, 仍未確定 A, B, C 之值. 所以在 SSS
的情形使用餘弦定理較合適.
即知道兩邊長及其夾角 (本題就是這樣的情況),
也就是說我們知道兩邊 a, c 以及夾角 B 之值或是 b, a 及 C 或是
c, b 及 A 之值. 我們舉知道 a, c, B 為例, 此時利用餘弦定理馬上知道
b = 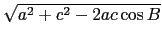 . 既然知道 a, b, c 之值了, 我們就可回到
SSS 的情形(用餘弦定理)求出另外兩個角 A, C. 要注意, 一開始處理 SAS
的情形時, 正弦定理幾乎派不上用場. 不過在求得第三邊後,
我們就可利用正弦定理求得各角的正弦值. 例如我們目前處理的情形(即知道
a, c, B 之值), 求出 b 值後我們就可利用正弦求出
sin A = (a/b)sin B 以及
sin C = (c/b)sin B. 這裡由於我們知道其中一個角為何,
所以不像單純的 SSS 之情形僅得
sin A, sin B, sin C 之比值,
而是正確的求出它們的值. 這個看法對處理這一題很有幫助.
即知道任兩角及任一邊的情形.
因為三角形三內角和為 180o, 知道兩個角即知道第三個角,
所以在這個情況之下已知的邊和角的相關位置並不重要. 我們舉知道三內角
A, B, C 以及一邊長 a 之值為例. 此時利用正弦定理可得
b = a(sin B)/(sin A) 以及
c = a(sin C)/(sin A), 因而確定了這個三角形.
當然了我們也可利用餘弦定理得到 b, c 的聯立方程式,
不過這是二次的聯立方程式, 處理起來較複雜,
所以此情況以正弦定理處理較合適.
. 既然知道 a, b, c 之值了, 我們就可回到
SSS 的情形(用餘弦定理)求出另外兩個角 A, C. 要注意, 一開始處理 SAS
的情形時, 正弦定理幾乎派不上用場. 不過在求得第三邊後,
我們就可利用正弦定理求得各角的正弦值. 例如我們目前處理的情形(即知道
a, c, B 之值), 求出 b 值後我們就可利用正弦求出
sin A = (a/b)sin B 以及
sin C = (c/b)sin B. 這裡由於我們知道其中一個角為何,
所以不像單純的 SSS 之情形僅得
sin A, sin B, sin C 之比值,
而是正確的求出它們的值. 這個看法對處理這一題很有幫助.
即知道任兩角及任一邊的情形.
因為三角形三內角和為 180o, 知道兩個角即知道第三個角,
所以在這個情況之下已知的邊和角的相關位置並不重要. 我們舉知道三內角
A, B, C 以及一邊長 a 之值為例. 此時利用正弦定理可得
b = a(sin B)/(sin A) 以及
c = a(sin C)/(sin A), 因而確定了這個三角形.
當然了我們也可利用餘弦定理得到 b, c 的聯立方程式,
不過這是二次的聯立方程式, 處理起來較複雜,
所以此情況以正弦定理處理較合適.
三角形的邊角關係還有兩種是不能確定唯一的三角形的,
我們依然可用正弦或餘弦定理探討其可能的情形.
即知道三個角 A, B, C. 其實三角形的三內角合為
180o, 所以知道三個角和僅知兩個角是等價的. 由於所給的訊息少,
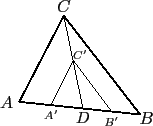
我們可以預期這樣的已知條件可得的三角形會有很多. 下圖就告訴我們,
給定一個三角形, 我們可在
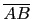 邊上任取一點 D, 再分別取
邊上任取一點 D, 再分別取
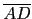 ,
,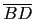 ,
,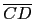 的中點為 A', B', C', 如此所得的三角形
A'B'C' (依相似三角形性質)和三角形 ABC 有相同的三個內角.
這時候我們可利用正弦定理得到 a : b : c 的比值, 即
a : b : c = sin A : sin B : sin C. 也就是說若給定三角形的三個內角,
則我們可確定三邊長的比值而不是三邊長. 反之若給了三邊長的比值,
我們可利用餘弦定理確定三個角的餘弦值, 也就是說確定了三個角.
所以知道三角形的三個角等價於知道三角形的三邊長之比值.
即知道兩邊長及其夾角之外的另一個角.
例如知道兩邊 a, b 以及夾角以外的角 A 或是角 B. 其他還有知道
a, c, A 之值, a, c, C 之值, b, c, B 之值或是 b, c, C 之值, 都是 SSA
的情形. 雖然同為知道兩邊一角, 但與 SAS 不同的是 SSA
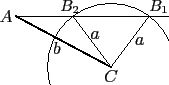
有可能得到兩個不相等的三角形. 下圖中是已知 a, b, A 的情形, 其中
a > b sin A. 我們以 C 點為圓心 a 為半徑畫圓,
如此所得的兩個三角形 AB1C 和 AB2C 不相等卻對應到同樣的 a, b, A
值.
的中點為 A', B', C', 如此所得的三角形
A'B'C' (依相似三角形性質)和三角形 ABC 有相同的三個內角.
這時候我們可利用正弦定理得到 a : b : c 的比值, 即
a : b : c = sin A : sin B : sin C. 也就是說若給定三角形的三個內角,
則我們可確定三邊長的比值而不是三邊長. 反之若給了三邊長的比值,
我們可利用餘弦定理確定三個角的餘弦值, 也就是說確定了三個角.
所以知道三角形的三個角等價於知道三角形的三邊長之比值.
即知道兩邊長及其夾角之外的另一個角.
例如知道兩邊 a, b 以及夾角以外的角 A 或是角 B. 其他還有知道
a, c, A 之值, a, c, C 之值, b, c, B 之值或是 b, c, C 之值, 都是 SSA
的情形. 雖然同為知道兩邊一角, 但與 SAS 不同的是 SSA
有可能得到兩個不相等的三角形. 下圖中是已知 a, b, A 的情形, 其中
a > b sin A. 我們以 C 點為圓心 a 為半徑畫圓,
如此所得的兩個三角形 AB1C 和 AB2C 不相等卻對應到同樣的 a, b, A
值.
我們舉知道兩邊 a, b 和角 A 為例. 例用正弦定理可得
sin B = (b/a)sin A. 所以若取一銳角  滿足
sin
滿足
sin = (b/a)sin A (注意因為
sin
= (b/a)sin A (注意因為
sin
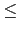 1, 所以只有當
a
1, 所以只有當
a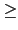 b sin A
才可找到此銳角
b sin A
才可找到此銳角  ), 則 B =
), 則 B =  或
B = 180o -
或
B = 180o -  .
對於這兩個可能的 B (當
.
對於這兩個可能的 B (當
 = 90o 即 a = b sin A 時,
僅有一個 B), 我們找到相對應的 C, 即
= 90o 即 a = b sin A 時,
僅有一個 B), 我們找到相對應的 C, 即
C = 180
o - (
A +
B) =
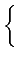
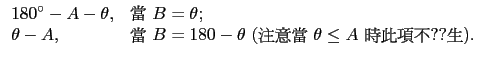
由於 A 是鈍角或直角時  不可能大於 A;
而當 A 是銳角時
不可能大於 A;
而當 A 是銳角時  > A 若且唯若
sin
> A 若且唯若
sin > sin A, 故由
sin
> sin A, 故由
sin = (b/a)sin A 知 b > a. 由此我們得知當給定 a, b, A 時, 只有在 A 是銳角且
b > a > b sin A 才會有兩個三角形滿足給定的 a, b, A 邊角關係之情形. 不管怎樣,
當我們得到可能的 B 值後, 三角形的三個角就知道了,
剩下的 c 值就可以用正弦定理
c = a(sin A/sin C) 或是餘弦定理
c =
= (b/a)sin A 知 b > a. 由此我們得知當給定 a, b, A 時, 只有在 A 是銳角且
b > a > b sin A 才會有兩個三角形滿足給定的 a, b, A 邊角關係之情形. 不管怎樣,
當我們得到可能的 B 值後, 三角形的三個角就知道了,
剩下的 c 值就可以用正弦定理
c = a(sin A/sin C) 或是餘弦定理
c = 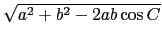 得到了. 其實 SSA
的情形也可以一開始用餘弦定理處理. 例如在知道 a, b, A 的情形,
我們可利用餘弦定理知, x = c 需滿足二次方程式
x2 - (2b cos A)x + (b2 - a2) = 0. 由判別式得知此二次方程式在
a
得到了. 其實 SSA
的情形也可以一開始用餘弦定理處理. 例如在知道 a, b, A 的情形,
我們可利用餘弦定理知, x = c 需滿足二次方程式
x2 - (2b cos A)x + (b2 - a2) = 0. 由判別式得知此二次方程式在
a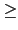 b sin A
時才會有實數解 (亦即才有可能得到三角形), 且在此時其根為
x = b cos A±
b sin A
時才會有實數解 (亦即才有可能得到三角形), 且在此時其根為
x = b cos A±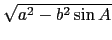 . 但 c 需為正數, 而此二次方程式在 A 為銳角時 (即
cos A > 0) 且
b > a > b sin A 時才會有兩個相異正實根.
這和前面用正弦定理推導的情形一致,
不過此時我們是找到三角形可能的三邊長, 所以最後要依 SSS
的情形用餘弦定理將另外兩個角求出.
. 但 c 需為正數, 而此二次方程式在 A 為銳角時 (即
cos A > 0) 且
b > a > b sin A 時才會有兩個相異正實根.
這和前面用正弦定理推導的情形一致,
不過此時我們是找到三角形可能的三邊長, 所以最後要依 SSS
的情形用餘弦定理將另外兩個角求出.
現在回到我們的問題. 題目中 c = 8,
b = 4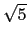 , 而
cos A = 1/
, 而
cos A = 1/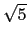 , 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a =
, 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a = 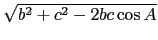 =
= 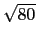 , 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C =
, 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C = 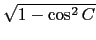 = 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/
= 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/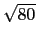 )(2/
)(2/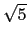 ) = 4/5. 另外眼尖的同學可由
a = b = 4
) = 4/5. 另外眼尖的同學可由
a = b = 4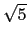 知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/
知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/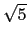 )(1/
)(1/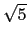 ) = 4/5.
) = 4/5.


下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: A
Li
2008-08-16
![]() ,
,![]() ,
,![]() ) 的邊長, 如下圖所示.
) 的邊長, 如下圖所示. 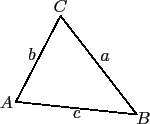
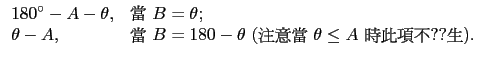
![]() , 而
cos A = 1/
, 而
cos A = 1/![]() , 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a =
, 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a = ![]() =
= ![]() , 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C =
, 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C = ![]() = 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/
= 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/![]() )(2/
)(2/![]() ) = 4/5. 另外眼尖的同學可由
a = b = 4
) = 4/5. 另外眼尖的同學可由
a = b = 4![]() 知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/
知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/![]() )(1/
)(1/![]() ) = 4/5.
) = 4/5.