

下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: 4. AAA
即知道兩邊長及其夾角之外的另一個角.
例如知道兩邊 a, b 以及夾角以外的角 A 或是角 B. 其他還有知道
a, c, A 之值, a, c, C 之值, b, c, B 之值或是 b, c, C 之值, 都是 SSA
的情形. 雖然同為知道兩邊一角, 但與 SAS 不同的是 SSA
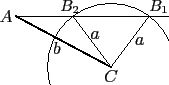
有可能得到兩個不相等的三角形. 下圖中是已知 a, b, A 的情形, 其中
a > b sin A. 我們以 C 點為圓心 a 為半徑畫圓,
如此所得的兩個三角形 AB1C 和 AB2C 不相等卻對應到同樣的 a, b, A
值.
我們舉知道兩邊 a, b 和角 A 為例. 例用正弦定理可得
sin B = (b/a)sin A. 所以若取一銳角  滿足
sin
滿足
sin = (b/a)sin A (注意因為
sin
= (b/a)sin A (注意因為
sin
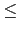 1, 所以只有當
a
1, 所以只有當
a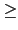 b sin A
才可找到此銳角
b sin A
才可找到此銳角  ), 則 B =
), 則 B =  或
B = 180o -
或
B = 180o -  .
對於這兩個可能的 B (當
.
對於這兩個可能的 B (當
 = 90o 即 a = b sin A 時,
僅有一個 B), 我們找到相對應的 C, 即
= 90o 即 a = b sin A 時,
僅有一個 B), 我們找到相對應的 C, 即
C = 180
o - (
A +
B) =
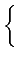
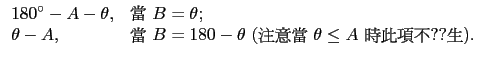
由於 A 是鈍角或直角時  不可能大於 A;
而當 A 是銳角時
不可能大於 A;
而當 A 是銳角時  > A 若且唯若
sin
> A 若且唯若
sin > sin A, 故由
sin
> sin A, 故由
sin = (b/a)sin A 知 b > a. 由此我們得知當給定 a, b, A 時, 只有在 A 是銳角且
b > a > b sin A 才會有兩個三角形滿足給定的 a, b, A 邊角關係之情形. 不管怎樣,
當我們得到可能的 B 值後, 三角形的三個角就知道了,
剩下的 c 值就可以用正弦定理
c = a(sin A/sin C) 或是餘弦定理
c =
= (b/a)sin A 知 b > a. 由此我們得知當給定 a, b, A 時, 只有在 A 是銳角且
b > a > b sin A 才會有兩個三角形滿足給定的 a, b, A 邊角關係之情形. 不管怎樣,
當我們得到可能的 B 值後, 三角形的三個角就知道了,
剩下的 c 值就可以用正弦定理
c = a(sin A/sin C) 或是餘弦定理
c = 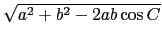 得到了. 其實 SSA
的情形也可以一開始用餘弦定理處理. 例如在知道 a, b, A 的情形,
我們可利用餘弦定理知, x = c 需滿足二次方程式
x2 - (2b cos A)x + (b2 - a2) = 0. 由判別式得知此二次方程式在
a
得到了. 其實 SSA
的情形也可以一開始用餘弦定理處理. 例如在知道 a, b, A 的情形,
我們可利用餘弦定理知, x = c 需滿足二次方程式
x2 - (2b cos A)x + (b2 - a2) = 0. 由判別式得知此二次方程式在
a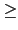 b sin A
時才會有實數解 (亦即才有可能得到三角形), 且在此時其根為
x = b cos A±
b sin A
時才會有實數解 (亦即才有可能得到三角形), 且在此時其根為
x = b cos A±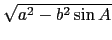 . 但 c 需為正數, 而此二次方程式在 A 為銳角時 (即
cos A > 0) 且
b > a > b sin A 時才會有兩個相異正實根.
這和前面用正弦定理推導的情形一致,
不過此時我們是找到三角形可能的三邊長, 所以最後要依 SSS
的情形用餘弦定理將另外兩個角求出.
. 但 c 需為正數, 而此二次方程式在 A 為銳角時 (即
cos A > 0) 且
b > a > b sin A 時才會有兩個相異正實根.
這和前面用正弦定理推導的情形一致,
不過此時我們是找到三角形可能的三邊長, 所以最後要依 SSS
的情形用餘弦定理將另外兩個角求出.
現在回到我們的問題. 題目中 c = 8,
b = 4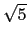 , 而
cos A = 1/
, 而
cos A = 1/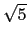 , 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a =
, 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a = 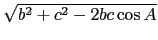 =
= 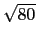 , 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C =
, 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C = 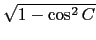 = 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/
= 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/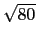 )(2/
)(2/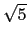 ) = 4/5. 另外眼尖的同學可由
a = b = 4
) = 4/5. 另外眼尖的同學可由
a = b = 4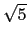 知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/
知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/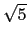 )(1/
)(1/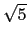 ) = 4/5.
) = 4/5.


下一頁: 四、非選擇題
上一頁: 三、選填題
前一頁: 4. AAA
Li
2008-08-16

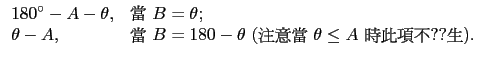
![]() , 而
cos A = 1/
, 而
cos A = 1/![]() , 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a =
, 是 SAS 的情形. 故依前面解說先利用餘弦定理得
a = ![]() =
= ![]() , 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C =
, 再依 SSS 的情形由餘弦定理得
cos C = (a2 + b2 - c2)/2ab = 3/5 而知
sin C = ![]() = 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/
= 4/5.
我們也可如 SAS 的解說中所述, 直接由正弦定理得
sin C = (c/a)sin A = (8/![]() )(2/
)(2/![]() ) = 4/5. 另外眼尖的同學可由
a = b = 4
) = 4/5. 另外眼尖的同學可由
a = b = 4![]() 知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/
知此三角形是等腰三角形而得
sin C = sin(180o - 2A) = sin(2A) = 2 sin A cos A = 2(2/![]() )(1/
)(1/![]() ) = 4/5.
) = 4/5.