
下一頁: 5. SSA
上一頁: 三、選填題
前一頁: 3. ASA 或 AAS
即知道三個角 A, B, C. 其實三角形的三內角合為
180o, 所以知道三個角和僅知兩個角是等價的. 由於所給的訊息少,
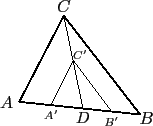
我們可以預期這樣的已知條件可得的三角形會有很多. 下圖就告訴我們,
給定一個三角形, 我們可在
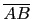 邊上任取一點 D, 再分別取
邊上任取一點 D, 再分別取
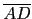 ,
,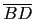 ,
,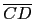 的中點為 A', B', C', 如此所得的三角形
A'B'C' (依相似三角形性質)和三角形 ABC 有相同的三個內角.
這時候我們可利用正弦定理得到 a : b : c 的比值, 即
a : b : c = sin A : sin B : sin C. 也就是說若給定三角形的三個內角,
則我們可確定三邊長的比值而不是三邊長. 反之若給了三邊長的比值,
我們可利用餘弦定理確定三個角的餘弦值, 也就是說確定了三個角.
所以知道三角形的三個角等價於知道三角形的三邊長之比值.
的中點為 A', B', C', 如此所得的三角形
A'B'C' (依相似三角形性質)和三角形 ABC 有相同的三個內角.
這時候我們可利用正弦定理得到 a : b : c 的比值, 即
a : b : c = sin A : sin B : sin C. 也就是說若給定三角形的三個內角,
則我們可確定三邊長的比值而不是三邊長. 反之若給了三邊長的比值,
我們可利用餘弦定理確定三個角的餘弦值, 也就是說確定了三個角.
所以知道三角形的三個角等價於知道三角形的三邊長之比值.
Li
2008-08-16