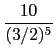(1) a > 0 (b) a < 1 (3) b < (1/6) (4) b < log10(4/3) (5) a > b
說明:本題將機率與對數相連結. 機率部分考的只有一個概念,
也就是樣本空間的一個分割內所對應的事件其發生的機率之總和為 1.
本題事實上主要就是考對數. 不過題目設計好像鼓勵學生背 log 3 和
log 2 的近似值. 雖然沒有記憶這些值仍可做答,
不過有記憶這些值的同學在時間上可能較占便宜.
這是因為若不是記憶這些值作答, 應該是先知道選項 (5) 的 a > b
再作答選項 (3) 問的 b 值是否小於 1/6 較合理.
依目前選項順序的安排, 是有可能浪費了沒有背這些值同學的作答時間.
若已知
log 3 ![]() 0.4771 以及
log 2
0.4771 以及
log 2 ![]() 0.3010
直接代入計算即可. 這裡我們就依沒有記 log 3 和 log 2
的值的情形來處理. 首先 0 < a < 1 可由題意機率的概念知道, 或直接由
a = log(3/2) 以及 1 < 3/2 < 10 知道. 重要的是處理 b,
依前述的機率性質知
b = 1 - 5a = 1 - 5 log(3/2). 若不知 log(3/2) 之值,
要回答 b 是否小於 1/6 計算起來較複雜. 我們先處理選項 (4),
此處是和 log(4/3) 相比較, 所以我們再將
b = 1 - 5 log(3/2) 化成
0.3010
直接代入計算即可. 這裡我們就依沒有記 log 3 和 log 2
的值的情形來處理. 首先 0 < a < 1 可由題意機率的概念知道, 或直接由
a = log(3/2) 以及 1 < 3/2 < 10 知道. 重要的是處理 b,
依前述的機率性質知
b = 1 - 5a = 1 - 5 log(3/2). 若不知 log(3/2) 之值,
要回答 b 是否小於 1/6 計算起來較複雜. 我們先處理選項 (4),
此處是和 log(4/3) 相比較, 所以我們再將
b = 1 - 5 log(3/2) 化成