5

給定二次多項式 f (x) = x² + ax + b，已知多項式 x³ + 3x² + 4x + 2 除以 f (x) 其餘式為 3x + 2，多項式 x³ + x² - x - 1 除以 f (x) 其餘式為 4x + 1，請選出正確的選項。

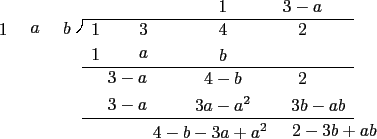
(1) a = 3                                (2) b = - 1                                 (3) 方程式 f (x) = 0 無實根

(4) f (x) 的極小值為 5/4    (5) f (x) 除以 (x + 3) 其餘式為 1.

說明:本題幾乎考了所有多項式應知道的觀念, 包括除法原理 (公因式), 餘式定理, 二次多項式根的判別以及極值. 雖然考的東西多, 不過並不難, 按部就班處理應該沒問題.

題目一開始的問題就表明要把 f (x) 求出來. 一般來說, 若給被除式以及除式, 我們很快就可以算出餘式. 本題是倒過來問, 給你被除式以及餘式問你除式為何. 從前我們提過這種倒過來的問題的處理原則, 也就是不妨將未知的東西當成已知直接操作. 本題除式 f (x) = x² + ax + b 雖為未知, 我們依然可以將 a, b 視為實數來操作, 也就是說用大家慣用的長除法求出餘式. 經長除法,

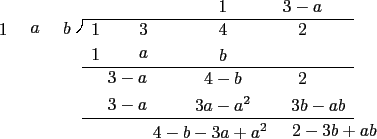
我們可以得到 x³ + 3x² + 4x + 2 除以 x² + ax + b 其餘式為 (4 - b - 3a + a²)x + (2 - 3b + ab). 同理可得, x³ + x² - x - 1 除以 x² + ax + b 其餘式為 (- 1 - b - a + a²)x + (- 1 - b + ab). 所以依題意知

(4 - b - 3a + a²)x + (2 - 3b + ab) = 3x + 2    以及    (- 1 - b - a + a²)x + (- 1 - b + ab) = 4x + 1,

也就是說 a, b 必須符合以下的聯立方程式:

$$\left\{\vphantom{ \begin{array}{ll} 4-b-3a+a^2 &=3 \qquad\qquad ... ...\qquad\qquad (3) \\ -1-b+ab &=1 \qquad\qquad (4) \\ \end{array}%% }\right.$$$$\begin{array}{ll} 4-b-3a+a^2 &=3 \qquad\qquad (1) \\ 2-3b+ab ... ...-a+a^2 &=4 \qquad\qquad (3) \\ -1-b+ab &=1 \qquad\qquad (4) \\ \end{array}$$

從 (2) 式我們得到 b(a - 3) = 0 也就是說 b = 0 或 a = 3. 不過若 b = 0 則代入 (4) 式得到矛盾, 故知 a = 3, 再代入 (4) 式得 b = 1. 又因為 a = 3, b = 1 也符合 (1)(3) 二式, 故知 a = 3, b = 1 為所求, 即 f (x) = x² + 3x + 1. 得到 f (x), 後面選項就好處理了. 我們可由 f (x) 的判別式大於 0, 或用配方法 f (x) = (x + (3/2))² - (5/4) 知道 f (x) 的極小值為 -5/4, 而由函數圖形得知 f (x) = 0 有兩相異實根. 最後我們可以再用一次長除法或直接套用餘式定理知 f (x) 除以 x + 3 的餘式應為 f (- 3) = (- 3)² + 3(- 3) + 1 = 1.

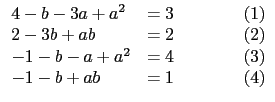
上面這個方法比較直接, 不過缺點是牽涉到要解聯立方程式, 還好本題要解的聯立方程式並不難, 否則要耽誤更多時間. 本題另一個處理方法還是用除法原理, 也就是說 x³ + 3x² + 4x + 2 除以 f (x) 其餘式為 3x + 2, 表示存在一個(一次)多項式 g(x) 使得 x³ + 3x² + 4x + 2 = g(x)f (x) + (3x + 2). 移項得 (x³ + 3x² + 4x + 2) - (3x + 2) = g(x)f (x). 換言之, f (x) 會是 (x³ + 3x² + 4x + 2) - (3x + 2) = x³ + 3x² + x 的因式. 同理 f (x) 也會是 (x³ + x² - x - 1) - (4x + 1) = x³ + x² - 5x - 2 的因式. 所以知 f (x) 會是 x³ + 3x² + x 和 x³ + x² - 5x - 2 的一個(二次的)公因式. 由於 x³ + 3x² + x 和 x³ + x² - 5x - 2 皆為三次多項似且並非差個常數倍, 所以它們的最高公因式絕不會是三次多項式. 而題目假設 f (x) = x² + ax + b 是一個(最高次項係數為 1 的)二次多項式, 故知 f (x) 必為 x³ + 3x² + x 和 x³ + x² - 5x - 2 的(最高次項係數為 1 的)最高公因式. 所以我們可以用多項式的輾轉相除法得到其(最高次項係數為 1 的)最高公因式為 x² + 3x + 1. 我們也可以用因式分解 x³ + 3x² + x = x(x² + 3x + 1) 以及 x³ + x² - 5x - 2 = (x - 2)(x² + 3x + 1) 看出 x² + 3x + 1 為其最高公因式. 因此求得 f (x) = x² + 3x + 1.