一

設 p(x) 為三次實係數多項式函數，其圖形通過 (1, 3),(- 1, 5) 兩點。若 p(x) 的圖形在點 (1, 3) 的切線斜率為 7，而在點 (- 1, 5) 的切線斜率為 -5，試求 p(x).

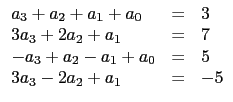
說明:本題是常見的三次多項式問題. 由於三次多項式共有四項係數, 所以需有四個條件才能完全決定這個三次多項式. 因此本題完全就是看能否知道如何用到這四個條件.

這又是一個倒著出的問題, 基本上若是給定一個多項式函數, 我們馬上可以知道其圖形可通過哪些點及在該點的切線斜率. 現在我們既然不知此三次多項式為何, 就大膽假設 p(x) = a₃x³ + a₂x² + a₁x + a₀. 由題意 y = p(x) 的圖形通過 (1, 3) 且在 (1, 3) 的切線斜率為 7, 故知 p(1) = 3 且 p'(1) = 7. 因此我們有 a₃ + a₂ + a₁ + a₀ = 3, 且因 p'(x) = 3a₃x² + 2a₂x + a₁, 故得 3a₃ + 2a₂ + a₁ = 7. 同理知 p(- 1) = 5 且 p'(- 1) = - 5, 故得 - a₃ + a₂ - a₁ + a₀ = 5 且 3a₃ - 2a₂ + a₁ = - 5. 整個問題就變成要解聯立方程式:

$$\left\{\vphantom{ \begin{array}{lcl} a_3+a_2+a_1+a_0&=&3 \\ 3... ... \\ -a_3+a_2-a_1+a_0&=&5\\ 3a_3-2a_2+a_1&=&-5 \\ \end{array}%% }\right.$$$$\begin{array}{lcl} a_3+a_2+a_1+a_0&=&3 \\ 3a_3+2a_2+a_1&=&7 \\ -a_3+a_2-a_1+a_0&=&5\\ 3a_3-2a_2+a_1&=&-5 \\ \end{array}$$

雖然有四個未知數, 不過由於係數並不複雜, 我們很容易用加減消去法解得 p(x) = x³ + 3x² - 2x + 1.

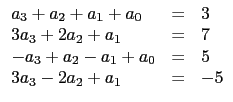
其時我們可以用餘式定理減少未知數的個數. 因 p(x) 是三次多項式, 由 p(1) = 3, 我們知存在一個二次多項式 h(x) = ax² + bx + c 使得 p(x) = h(x)(x - 1) + 3, 亦即 p(x) = (ax² + bx + c)(x - 1) + 3. 此時我們僅有三個未知數要處理 (即 a, b, c). 不過這裡要求 p'(x) 或許同學覺得要乘開再微分頗麻煩. 但若知道微分的乘法公式 (即 f (x)g(x) 的微分為 f'(x)g(x) + f (x)g'(x)) 就簡單多了, 可得 p'(x) = (ax² + bx + c) + (2ax + b)(x - 1). 因此由剩下 p'(1) = 7, p(- 1) = 5 和 p'(- 1) = - 5 這三個條件, 我們只要解以下的聯立方程式:

$$\left\{\vphantom{ \begin{array}{lcl} a+b+c&=&7 \\ -2a+2b-2c+3&=&5\\ 5a-3b+c&=&-5 \\ \end{array}%% }\right.$$$$\begin{array}{lcl} a+b+c&=&7 \\ -2a+2b-2c+3&=&5\\ 5a-3b+c&=&-5 \\ \end{array}$$

解之得 a = 1, b = 4, c = 2.

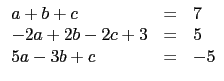
另外結合綜合除法的概念, 我們可以將 p(x) 寫成 p(x) = r(x - 1)³ + s(x - 1)² + t(x - 1) + 3, 這樣也將問題化成三個未知數的形式. 同樣的若要將整個式子乘開再微分也很複雜, 不過若知道當 n$\ge$2 時 (x - 1)ⁿ 的微分為 n(x - 1)^{n - 1}, 這樣就簡單了. 此時, p'(x) = 3r(x - 1)² + 2s(x - 1) + t, 所以很容易知道 t = p'(1) = 7. 因此我們只要解 r, s 即可. 利用 p(- 1) = 5 且 p'(- 1) = - 5, 知 r, s 需符合 -8r + 4s - 14 + 3 = 5 以及 12r - 4s + 7 = - 5, 故解聯立方程式得 r = 1, s = 6. 從前面的推導, 我們可以知道當 p(x) 是三次多項式時, 可以將 p(x) 寫成 p(x) = r(x - 1)³ + s(x - 1)² + p'(1)(x - 1) + p(1). 事實上可推出 r, s 分別和 p'''(1) 以及 p''(1) 有關, 這就是大學微積分課程中所謂的泰勒展開式.