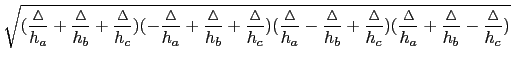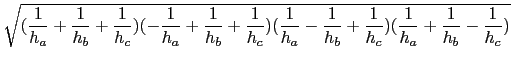二

設 $\vartriangle$ABC 的三高分別為 $\overline{AD}$ = 6、 $\overline{BE}$ = 4、 $\overline{CF}$ = 3。

(1) 試證： $\vartriangle$ABC 是一鈍角三角形。

(2) 試求 $\vartriangle$ABC 的面積。

說明:這是一個三角的問題, 比較不同的是, 這個三角形不是由邊角關係來確認, 而是由高來決定. 所以必須將高的關係轉換成邊角關係來處理.

為了方便起見, 我們將三角形三個角 A, B, C 的角度直接設為 A, B, C 且其對邊邊長 $\overline{BC}$,$\overline{AC}$,$\overline{AB}$ 分別設為 a, b, c. 而 a, b, c 邊上的高 $\overline{AD}$,$\overline{BE}$,$\overline{CF}$ 分別設為 h_a, h_b, h_c. 依題意, 我們有 h_a = 6, h_b = 4, h_c = 3.

要如何利用高找到邊角關係呢? 最直接的就是 c sin B = b sin C = h_a, c sin A = a sin C = h_b 以及 a sin B = b sin A = h_c. 由此我們可以得 c/a = h_a/h_c = 2, b/a = h_a/h_b = 3/2 (以及 c/b = h_b/h_c = 4/3), 故有 a : b : c = 1 : 3/2 : 2 = 2 : 3 : 4. (同理我們也可得 sin A : sin B : sin C = 2 : 3 : 4, 不過這由正弦定理亦可得, 並沒給我們什麼新的訊息. 更何況正弦值無法判定角度是否為鈍角, 所以我們可先不管這個正弦的比值.) 另外利用高和邊長我們可得三角形面積, 所以若此三角形面積為 $\vartriangle$, 則我們有 ah_a = bh_b = ch_c = 2$\vartriangle$. 由此我們同樣可得 a : b : c = 2 : 3 : 4.

現在我們知道此三角形三邊長的比值, 由三角形邊角關係(利用餘弦定理)這等於告訴我們此三角形的三個角. (對此不熟悉的同學, 建議參考``97 學年指考數學乙''選填題 C 的解說.) 會考慮用餘弦定理的另一個原因是, 餘弦值可判定一個角是否為鈍角(以便回答第一個問題). 故利用餘弦定理知

cos A = $${\frac{b^2+c^2-a^2}{2bc}}$$ = $${\textstyle\frac{7}{8}}$$,    cos B = $${\frac{a^2+c^2-b^2}{2ac}}$$ = $${\textstyle\frac{11}{16}}$$,    cos C = $${\frac{a^2+b^2-c^2}{2ab}}$$ = $${\frac{-1}{4}}$$

由於 cos C < 0, 知 C 為鈍角, 所以 $\vartriangle$ABC 為鈍角三角形.

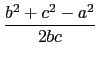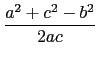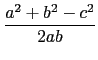要求三角形面積, 就必須確定這個三角形, 也就是說不只要知道三個角還要確定三邊長. 此時我們已可由 cos A, cos B, cos C 之值確定 sin A, sin B, sin C 之值 (注意是值而不僅是比值). 因此可由前 b sin C = h_a 來求出 b 之值 (進而得 a, c 之值). 也就是說, 因為 sin C = $\sqrt{1-\cos^2C}$ = $\sqrt{15/16}$, 我們有 b = h_a/sin C = 6/$\sqrt{15/16}$ = 24/$\sqrt{15}$. 再由 $\vartriangle$ = bh_b/2 得此三角形面積為 48/$\sqrt{15}$ = 16$\sqrt{15}$/5.

看到三角形面積, 許多同學會想到 Heron (海龍)公式. 我們也可利用海龍公式, 求出此三角形面積. 事實上由前 a = 2$\vartriangle$/h_a, b = 2$\vartriangle$/h_b, c = 2$\vartriangle$/h_c, 利用海龍公式可得

$$\vartriangle$$ = $$\sqrt{(\frac{\vartriangle}{h_a}+\frac{\vartriangle}{h_b}+\frac{\v... ... (\frac{\vartriangle}{h_a}+\frac{\vartriangle}{h_b}-\frac{\vartriangle}{h_c})}$$

將根號內的 $\vartriangle$ 提出相約後, 我們可得

$$\vartriangle$$ = $$\left(\vphantom{\sqrt{(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c})... ...{1}{h_b}+\frac{1}{h_c}) (\frac{1}{h_a}+\frac{1}{h_b}-\frac{1}{h_c})}\,}\right.$$$$\sqrt{(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}) (-\frac{1}{h_a... ...h_a}-\frac{1}{h_b}+\frac{1}{h_c}) (\frac{1}{h_a}+\frac{1}{h_b}-\frac{1}{h_c})}$$ $$\left.\vphantom{\sqrt{(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c})... ...+\frac{1}{h_c}) (\frac{1}{h_a}+\frac{1}{h_b}-\frac{1}{h_c})}\,}\right)^{-1}_{}$$

這是用高來寫下的海龍公式.