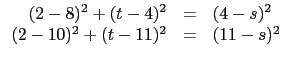(1) 若拋物線 ![]() 的頂點坐標為 (2, 1),則其焦點坐標必為 (2, 4)
的頂點坐標為 (2, 1),則其焦點坐標必為 (2, 4)
(2) 若拋物線 ![]() 的焦點坐標為 (2, 12),則其頂點坐標必為 (2, 3)
的焦點坐標為 (2, 12),則其頂點坐標必為 (2, 3)
(3) 若拋物線 ![]() 也通過點 (10, 11),則其準線方程式必為 y + 6 = 0
也通過點 (10, 11),則其準線方程式必為 y + 6 = 0
(4) 直線 x - 2 = 0 上每個點都可能是拋物線 ![]() 的頂點
的頂點
(5) 直線 x - 2 = 0 上每個點都可能是拋物線 ![]() 的焦點
的焦點
說明:本題仍為標準形式的拋物線,
基本上若能寫下符合題意的拋物線方程式的通式就能解題.
不過五個選項皆為獨立, 對許多同學來說等於做五個題目, 解題比較費時.
事實上有些選項若能搭配拋物線的定義來解, 就輕鬆多了.
二次曲線的問題有時(標準型)可用其方程式來解題, 但有時用定義來解較容易. 本題若能適時搭配兩種解法, 處理起來會比較輕鬆. 這裡我們試著每個選項都用這兩種方式處理, 讓大家體會這兩種處理方式的適用時機.
所謂一個拋物線的方程式, 就是此拋物線上的點都會滿足的方程式,
反之滿足方程式的點都會在這個拋物線上. 本題中拋物線 ![]() 的對稱軸為 x = 2, 所以頂點坐標應為 (2, b), 其中 b 為實數.
若拋物線的焦距為 c, 因
的對稱軸為 x = 2, 所以頂點坐標應為 (2, b), 其中 b 為實數.
若拋物線的焦距為 c, 因 ![]() 為開口往上或往下
(因對稱軸為鉛直線) 所以其方程式為
(x - 2)2 = 4c(y - b). 現已知
為開口往上或往下
(因對稱軸為鉛直線) 所以其方程式為
(x - 2)2 = 4c(y - b). 現已知 ![]() 通過 (8, 4) 故有
(8 - 2)2 = 4c(4 - b),
即 4c - bc = 9. 也就是說依題幹, 我們已有 b, c 的一個關係式, 我們需要另一個關係式來確定
b, c. 只要 b, c 確定了就確認了這一個拋物線
通過 (8, 4) 故有
(8 - 2)2 = 4c(4 - b),
即 4c - bc = 9. 也就是說依題幹, 我們已有 b, c 的一個關係式, 我們需要另一個關係式來確定
b, c. 只要 b, c 確定了就確認了這一個拋物線 ![]() . 既然
. 既然 ![]() 的方程式描述的是
的方程式描述的是 ![]() 上的點,
所以當問題的訊息是有關
上的點,
所以當問題的訊息是有關 ![]() 上的點, 那麼此方程式就很好用.
例如選項 (1), (3), (4) 都是有關
上的點, 那麼此方程式就很好用.
例如選項 (1), (3), (4) 都是有關 ![]() 上的點,
所以用方程式來處理應較有效. 選項 (1) 給的是頂點坐標 (頂點當然是
上的點,
所以用方程式來處理應較有效. 選項 (1) 給的是頂點坐標 (頂點當然是
![]() 上的點), 依此我們知 b = 1, 套回 b, c 的關係式知 c = 3.
再由 c = 3 得知焦點的 y 軸坐標為 b + c = 1 + 3 = 4, 故焦點坐標為
(2, 4). 選項 (3) 給的是
上的點), 依此我們知 b = 1, 套回 b, c 的關係式知 c = 3.
再由 c = 3 得知焦點的 y 軸坐標為 b + c = 1 + 3 = 4, 故焦點坐標為
(2, 4). 選項 (3) 給的是 ![]() 上的另一點 (10, 11), 所以代入
上的另一點 (10, 11), 所以代入
![]() 的方程式得
(10 - 2)2 = 4c(11 - b), 即 11c - bc = 16.
解聯立方程式
的方程式得
(10 - 2)2 = 4c(11 - b), 即 11c - bc = 16.
解聯立方程式
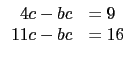
選項 (2), (5) 的訊息為焦點. 焦點不在拋物線上, 故若要用方程式來處理,
就必須將焦點的訊息轉換成拋物線上的點 (一般就是頂點,
因為它和焦點關係最密切). 將焦點坐標 (2, 12) 轉換成頂點坐標, 頂點之
y 軸坐標應為 12 - c (因已假設焦距為 c), 即 b = 12 - c. 代回原已知
b, c 的關係式 4c - bc = 9, 得 c 需滿足
c2 - 8c - 9 = 0, 即 c = 9 或
c = - 1. 故知這樣的 ![]() 應有兩個, 一個頂點為 (2, 3),
另一個頂點為 (2, 13). 選項 (5) 是選項 (2) 的``一般版",
問是否對任意給定的實數 r, 皆可找到一滿足題幹的拋物線其焦點坐標為
(2, r)? 然而若
應有兩個, 一個頂點為 (2, 3),
另一個頂點為 (2, 13). 選項 (5) 是選項 (2) 的``一般版",
問是否對任意給定的實數 r, 皆可找到一滿足題幹的拋物線其焦點坐標為
(2, r)? 然而若 ![]() 的焦點坐標為 (2, r), 則
的焦點坐標為 (2, r), 則 ![]() 的頂點坐標應為 (2, r - c), 即 b = r - c. 故由 b, c 需滿足 4c - bc = 9
的關係式, 得 c 需滿足
c2 + (4 - r)c - 9 = 0. 由於此二次方程式判別式
(4 - r)2 + 36 恆大於 0, 知對任意給定的實數 r, 皆可找到(兩個相異)
實數解, 亦即必存在(兩個)滿足題幹的拋物線其焦點為 (2, r).
的頂點坐標應為 (2, r - c), 即 b = r - c. 故由 b, c 需滿足 4c - bc = 9
的關係式, 得 c 需滿足
c2 + (4 - r)c - 9 = 0. 由於此二次方程式判別式
(4 - r)2 + 36 恆大於 0, 知對任意給定的實數 r, 皆可找到(兩個相異)
實數解, 亦即必存在(兩個)滿足題幹的拋物線其焦點為 (2, r).
所謂拋物線的定義指的是每一條拋物線都有一個焦點與一條準線,
而拋物線上的點到準線和焦點距離相等,
反之到準線和焦點距離相等的點都在此拋物線上. 所以只要準線和焦點確定,
這條拋物線也因之而確定了. 本題中 ![]() 的稱軸為鉛直線 x = 2,
所以我們知焦點會落在 x = 2 這直線上, 而準線會是與 x = 2
相垂直的一條水平線. 又已知
的稱軸為鉛直線 x = 2,
所以我們知焦點會落在 x = 2 這直線上, 而準線會是與 x = 2
相垂直的一條水平線. 又已知 ![]() 通過 (8, 4), 所以準線會是一個以
(8, 4) 為圓心的圓的一個水平切線, 而焦點會是此圓和直線 x = 2
的一個交點. 既然由焦點和準線可確定此拋物線, 所以當問題的訊息是有關
通過 (8, 4), 所以準線會是一個以
(8, 4) 為圓心的圓的一個水平切線, 而焦點會是此圓和直線 x = 2
的一個交點. 既然由焦點和準線可確定此拋物線, 所以當問題的訊息是有關
![]() 的焦點或準線, 那麼用定義會比較好處理. 例如選項 (2),
(5) 都是有關
的焦點或準線, 那麼用定義會比較好處理. 例如選項 (2),
(5) 都是有關 ![]() 的焦點, 所以用定義來處理應較有效. 選項 (2)
中已知焦點為 (2, 12) 所以我們可以 (8, 4) 為圓心, (8, 4) 到
(2, 12) 的距離 (即 10) 為半徑畫圓. 此圓有兩個水平切線 (即 y = - 6
與 y = 14), 也就是說 (8, 4) 到 (2, 12)
的距離和到這兩條水平線的距離皆相等. 換言之, 若以 (2, 12)
為焦點這兩條水平線都可能會是
的焦點, 所以用定義來處理應較有效. 選項 (2)
中已知焦點為 (2, 12) 所以我們可以 (8, 4) 為圓心, (8, 4) 到
(2, 12) 的距離 (即 10) 為半徑畫圓. 此圓有兩個水平切線 (即 y = - 6
與 y = 14), 也就是說 (8, 4) 到 (2, 12)
的距離和到這兩條水平線的距離皆相等. 換言之, 若以 (2, 12)
為焦點這兩條水平線都可能會是 ![]() 的準線. 因此符合條件的
的準線. 因此符合條件的
![]() 無法確定頂點會是哪一個 (所以選項 (2) 是錯的). 事實上若
y = - 6 為其準線, 則焦距為
(12 - (- 6))/2 = 9, 知頂點為 (2, 3), 但若
y = 14 為其準線, 則焦距為
(12 - 14)/2 = - 1, 得頂點為 (2, 13).
這個結果和前面用方程式的方法所得結果相吻合. 選項 (5) 是選項 (3)
的一般情況, 在 x = 2 上任取一點, 則以此點到 (8, 4) 的距離為半徑,
並以 (8, 4) 為圓心畫圓. 此圓必有兩條水平切線,
因而得知必可找到(兩條)準線. 也就是說以 x = 2
上任一點為焦點且符合題意的拋物線一定存在(且有兩條).
無法確定頂點會是哪一個 (所以選項 (2) 是錯的). 事實上若
y = - 6 為其準線, 則焦距為
(12 - (- 6))/2 = 9, 知頂點為 (2, 3), 但若
y = 14 為其準線, 則焦距為
(12 - 14)/2 = - 1, 得頂點為 (2, 13).
這個結果和前面用方程式的方法所得結果相吻合. 選項 (5) 是選項 (3)
的一般情況, 在 x = 2 上任取一點, 則以此點到 (8, 4) 的距離為半徑,
並以 (8, 4) 為圓心畫圓. 此圓必有兩條水平切線,
因而得知必可找到(兩條)準線. 也就是說以 x = 2
上任一點為焦點且符合題意的拋物線一定存在(且有兩條).
如果給的訊息是拋物線上另一點, 那麼用定義來處理就較麻煩了.
我們必須利用這個點來找出此拋物線的焦點和準線. 選項 (1)
給的是頂點坐標 (2, 1). 既然 (2, 1) 和 (8, 4) 在同一個拋物線上,
表示我們要找到兩個分別以 (2, 1) 和 (8, 4) 為圓心的圓,
其中有一個交點落在 x = 2 這條直線上 (因焦點必在對稱軸上)
且有共同的水平切線 (因準線是水平線). 這沒什麼好的幾何看法能處理,
僅能用代數的方法來解, 不過這就回歸到原來方程式的解法了.
也就是說我們假設 ![]() 的焦距為 c. 可得準線為 y = 1 - c, 焦點為
(2, 1 + c). 因 (8, 4) 到準線 y = 1 - c 的距離為
4 - (1 - c) = 3 + c, 知
(8, 4) 到焦點 (2, 1 + c) 的距離
的焦距為 c. 可得準線為 y = 1 - c, 焦點為
(2, 1 + c). 因 (8, 4) 到準線 y = 1 - c 的距離為
4 - (1 - c) = 3 + c, 知
(8, 4) 到焦點 (2, 1 + c) 的距離
![]() 應為
3 + c. 解得 c = 3, 得知焦點為 (2, 4). 選項 (4) 是選項 (1)
的一般情形, 我們可依上面的方法證得 (2, 4) 不可能為頂點,
這裡就不再贅述. 事實上由拋物線的圖形很容易知道 (2, 4) 不可能是頂點.
這是因為由對稱軸是鉛直線, 我們知
應為
3 + c. 解得 c = 3, 得知焦點為 (2, 4). 選項 (4) 是選項 (1)
的一般情形, 我們可依上面的方法證得 (2, 4) 不可能為頂點,
這裡就不再贅述. 事實上由拋物線的圖形很容易知道 (2, 4) 不可能是頂點.
這是因為由對稱軸是鉛直線, 我們知 ![]() 是開口向上或開口向下的拋物線, 所以不應有其他的點 (即 (8, 4))
和頂點是同樣高度的 (即 y 軸坐標皆為 4). 至於選項 (3) 已知
是開口向上或開口向下的拋物線, 所以不應有其他的點 (即 (8, 4))
和頂點是同樣高度的 (即 y 軸坐標皆為 4). 至於選項 (3) 已知
![]() 通過另外一點 (10, 11), 也就是說我們要找到兩個圓分別以
(8, 4) 和 (10, 11) 為圓心有共同的水平切線 (即
通過另外一點 (10, 11), 也就是說我們要找到兩個圓分別以
(8, 4) 和 (10, 11) 為圓心有共同的水平切線 (即 ![]() 的準線)
且兩圓有一交點 (即
的準線)
且兩圓有一交點 (即 ![]() 的焦點) 落在 x = 2 上.
我們假設此二圓共同的水平切線為 y = s, 且交於 x = 2 的點為 (2, t).
因為 (8, 4) 到 y = s 的距離為
的焦點) 落在 x = 2 上.
我們假設此二圓共同的水平切線為 y = s, 且交於 x = 2 的點為 (2, t).
因為 (8, 4) 到 y = s 的距離為
![]() 4 - s
4 - s![]() , 而 (10, 11) 到 y = s
的距離為
, 而 (10, 11) 到 y = s
的距離為
![]() 11 - s
11 - s![]() , 所以以 (8, 4) 為圓心的圓其半徑為
, 所以以 (8, 4) 為圓心的圓其半徑為
![]() 4 - s
4 - s![]() 而以 (10, 11) 為圓心的圓其半徑應為
而以 (10, 11) 為圓心的圓其半徑應為
![]() 11 - s
11 - s![]() . 焦點 (2, t)
必需在這兩個圓上, 所以我們有以下的聯立方程式:
. 焦點 (2, t)
必需在這兩個圓上, 所以我們有以下的聯立方程式: