
下一頁: 8
上一頁: 二、多選題
前一頁: 6
設 f'(x) 表示實係數多項式函數 f (x) 的導函數,已知
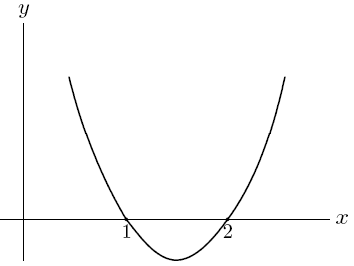
y = f'(x) 的圖形是一個通過點 (1, 0) 和點 (2, 0)
且開口向上的拋物線。試問下列哪些選項是正確的?
(1) f (x) 一定是三次多項式 (2) f (x) 在 1 < x < 2
的範圍內必為遞增
(3) f (x) 一定恰有兩個極值 (4) f (x) = 0 一定有三個實根
(5) f (x) = 0 在
1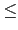 x
x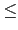 2 的範圍內一定有實根
2 的範圍內一定有實根
說明:本題是利用導函數的圖形來判讀原函數的圖形,
基本上只要了解導函數的正負取值和原函數的遞增遞減的關係以及導函數無法決定原函數的取值這兩個概念就能解題.
本題選項 (4) 和選項 (5) 問的是同一個概念, 浪費了一個選項有點可惜.
我們從題目給的 f'(x) 的訊息著手. 依題意 y = f'(x) 的圖形如下:
首先由 y = f'(x) 的圖形是拋物線知 f'(x) 是一個二次多項式, 故得知
f (x) 必為一個三次多項式. 接著由 y = f'(x) 通過 (1, 0) 和 (2, 0)
知 f'(1) = 0 且 f'(2) = 0. 再由 y = f'(x) 是開口向上的拋物線知當
1 < x < 2 時 f'(x) < 0; 而當 x < 1 或 x > 2 時 f'(x) > 0. 由此知
f (x) 在 1 < x < 2 的範圍內為遞減; 而 f (x) 在 x < 1 或 x > 2
的範圍內為遞增. 依此我們也可得知 f (x) 僅有在 x = 1 和 x = 2
時有極值. 事實上 f (x) 在 x = 1 有局部極大值, 而在 x = 1
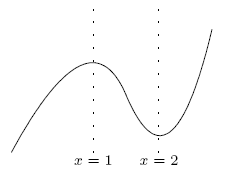
有局部極小值. 我們可以約略畫出 y = f (x) 的圖形如下:
大家都知道當 c 是一個常數時,
g(x) = f (x) + c 的導函數和 f (x)
的導函數是相同的 (更何況本題中 f'(x) 也未定),
所以上圖中我們無法決定 x
軸的位置. 也就是說選項 (4) 和選項 (5) 都是錯的. 事實由上面的圖形我們知本題中需知
f (1)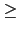 0 且 f (2)
0 且 f (2)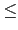 0 方能確保 f (x) = 0 有三實根,
也只有在這情況才能確保 f (x) = 0 在
1
0 方能確保 f (x) = 0 有三實根,
也只有在這情況才能確保 f (x) = 0 在
1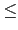 x
x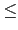 2 有實根.
2 有實根.
本題我們也可依
f'(x) = r(x - 1)(x - 2), 其中 r 為一正實數 (因
f'(1) = f'(2) = 0 且 y = f'(x) 圖形為開口向上的拋物線), 利用反導函數得
f (x) = (r/3)x3 - (3r/2)x2 + 2rx + c. 再找出反例知選項 (4), (5) 都是錯的.
例如當 r = 6 且 c = - 6 時,
f (x) = 2x3 - 9x2 + 12x - 6. 此時 f (x) = 0
僅有一實根且此實根大於 2 (因 f (1) < 0).


下一頁: 8
上一頁: 二、多選題
前一頁: 6
Li
2008-08-16
![]() x
x![]() 2 的範圍內一定有實根
2 的範圍內一定有實根