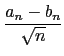 = 2
= 2
(1) an > 0 對所有 n 皆成立 (2) an + bn = 2 對所有 n 皆成立
(3) bn + 1 > bn 對所有 n 皆成立
(4)
![]()
![]() = 1
(5)
= 1
(5)
![]()
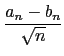 = 2
= 2
說明:本題基本上是考二次方程式的根以及根式的極限.
雖然有些選項可用根與係數關係處理,
不過有些選項問的是兩個不同方程式的根, 所以直接求出根來解比較容易.
若先從根與係數關係思考, 我們知 an + bn = 2 且 anbn = - n. 既然
anbn < 0 (n 是正整數) 且 an > bn, 依此可知 an > 0. 所以選項
(1), (2) 皆可由根與係數關係得知. 選項 (5) 也可由根與係數關係著手,
這是因為 an > bn 所以
an - bn = ![]() = 2
= 2![]() , 最後再求極限即可.
選項 (3),(4) 因考慮的是不同的方程式之根, 無法直接由根與係數關係判斷,
所以我們還是乖乖地將 an, bn 的通式求出較實際.
, 最後再求極限即可.
選項 (3),(4) 因考慮的是不同的方程式之根, 無法直接由根與係數關係判斷,
所以我們還是乖乖地將 an, bn 的通式求出較實際.
依公式解, 我們知
an = 1 + ![]() 且
bn = 1 -
且
bn = 1 - ![]() , 所以依
, 所以依
![]() 在 x > 0 時是遞增的知
bn = 1 -
在 x > 0 時是遞增的知
bn = 1 - ![]() > 1 -
> 1 - ![]() = bn + 1. 最後我們就是要探討選項 (4),
(5) 這兩個根式的極限, 順便討論一下極限的運算性質.
我們常用的極限運算性質如下: 假設
= bn + 1. 最後我們就是要探討選項 (4),
(5) 這兩個根式的極限, 順便討論一下極限的運算性質.
我們常用的極限運算性質如下: 假設
![]() an = a 且
an = a 且
![]() bn = b, 則我們有
bn = b, 則我們有
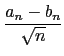 =
= 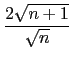 =
= 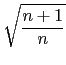 = 2.
= 2.
至於選項 (4) 由於
anan + 1/n 的分母當 n
趨近於無窮大時其極限不存在,
所以我們不能套用極限的除法性質處理這個極限. 但我們可以將
anan + 1/n 拆成
(an/![]() )(an + 1/
)(an + 1/![]() ), 且若能知道當
n 趨近於無窮大時
an/
), 且若能知道當
n 趨近於無窮大時
an/![]() 和
an + 1/
和
an + 1/![]() 的極限皆存在, 則我們可用極限的乘法性質得到此極限. 然而
an/
的極限皆存在, 則我們可用極限的乘法性質得到此極限. 然而
an/![]() = (1 +
= (1 + ![]() )/
)/![]() ,
我們依然不能用極限的除法性質, 所以再將
an/
,
我們依然不能用極限的除法性質, 所以再將
an/![]() 拆成
(1/
拆成
(1/![]() ) + (
) + (![]() /
/![]() ). 由於
). 由於
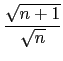 =
= 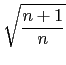 =
= 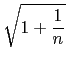 = 1.
= 1.
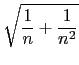 +
+ 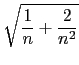 +
+ 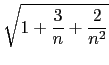 = 1
= 1
本題的所涉及的極限概念, 重點不在於它有根式, 而是它的分式.
根式的極限問題所用的 ![]() 的連續性, 大部分同學都能理解,
應該不困難. 而分式的極限就必須處理無法使用極限除法性質的情形,
也就是分母的極限不存在或為 0. 本題中由於分母是單項式,
所以我們將原分式化成一些分式的加法再用極限的加法性質處理.
當分式的分母不是單項式時, 就較麻煩了, 等我們以後碰到類似問題再探討.
的連續性, 大部分同學都能理解,
應該不困難. 而分式的極限就必須處理無法使用極限除法性質的情形,
也就是分母的極限不存在或為 0. 本題中由於分母是單項式,
所以我們將原分式化成一些分式的加法再用極限的加法性質處理.
當分式的分母不是單項式時, 就較麻煩了, 等我們以後碰到類似問題再探討.