5

某人進行一實驗來確定某運動之距離 d 與時間 t 的平方或立方成正比，所得數據如下：

時間 t (秒)	0.25	0.5	0.75	1	1.25	1.5	1.75	2	2.25
距離 d (呎)	0.95	3.69	9.71	14.88	22.32	39.34	48.68	53.65	71.79

為探索該運動的距離與時間之關係，令 x = log₂t， y = log₂d， 即將上述的數據 (t, d ) 分別取以 2 為底的對數變換，例如： (2, 53.65) 變換後成為 (1, 5.74)。已知變換後的數據 (x₁, y₁),(x₂, y₂),...,(x₉, y₉) 之散佈圖及以最小平方法所求得變數 y 對變數 x 的最適合直線（或稱迴歸直線）為 y = a + bx，如下圖所示：

試問下列哪些選項是正確的？

(1) 若 d = 14.88，則 3 < log₂d < 4    (2) x 與 y 的相關係數小於 0.2

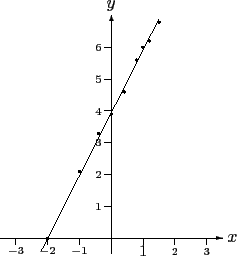
(3) 由上圖可以觀察出 b > 2.5            (4) 由上圖可以觀察出 a > 2

(5) 由上圖可以確定此運動之距離與時間的立方約略成正比

說明:本題主要是考對數, 不過又與迴歸直線和相關係數連結. 本題以多重選擇題型式出現, 大部分選項僅是直線圖形觀察, 而使原題重點失焦, 甚為可惜.

所謂 d 與 t 的 n 次方成正比, 表示存在 k 使得 d = kt ⁿ. 當我們不知 n, k 為何且有一組有關 d 和 t 的資料時, 若將它們以數對 (t, d ) 瞄點於以 t 為橫軸 d 為縱軸的坐標系時, 除非這些點排列很接近一直線(此時我們可知 n = 1 且 k 為斜率), 一般來說我們很難依這些點的排列估計 n 和 k 之值. 基於直線較易觀察及判斷的特點, 我們可以利用取對數的方法來估計 n 和 k 之值. 當我們取一個不為 1 的正數為底時, 例如本題以 2 為底, 令 x = log₂t 且 y = log₂d, 此時 d 與 t 的關係式 d = kt ⁿ 等式兩邊取對數 (即 log₂d = log₂(kt ⁿ) = log₂k + n log₂t), 可轉換成 y 與 x 的關係式 y = log₂k + nx. 因此若我們將前面 t, d 的資料轉換成 x, y 後, 將它們以數對 (x, y) 瞄點於以 x 為橫軸 y 為縱軸的坐標系時, 這些點會很接近一條直線. 這直線的斜率就是 n, 而其 y 軸截距會是 log₂k, 依此我們便可估計出 n, k 之值.

本題中的迴歸直線 y = a + bx, 就是要估計出數對 (x, y) 所接近的那條直線. 因此, 我們能依 a 值估計出 k (即 k $\approx$ 2^a) 且依 b 值估計出 n (即 n $\approx$ b). 選項 (1) 問的是當 d = 14.88 時有關 log₂d 之值的問題, 我們當然可由 2³ = 8 < 14.88 < 16 = 2⁴ 得知 3 < log₂d < 4. 我們也可由 t = 1 所對應的就是 d = 14.88 而知 x = log₂1 = 0 所對應的 y 值 (即 y 軸截距) 就是 log₂d, 由迴歸直線的 y 截距界於 3 和 4 之間, 我們也可得選項 (1) 是對的. 因為 a 值也就是 y 軸截距, 這也回答了選項 (4), 即 a > 2. 選項 (3) 問的 b 值, 就是迴歸直線的斜率. 依圖形 b 值應很接近 2, 所以 b 不應大於 2.5. 這也同時回答了選項 (5), 即 n 應該就是 2 而不是 3, 也就是說 d 與 t 的平方約略成正比而不是立方.

選項 (2) 問的是相關係數, 雖然題目中給了很多點, 但我們不必真的去求相關係數. 因為這些點皆在迴歸直線附近, 應為高度相關, 所以相關係數應較接近 1, 不會小於 0.2.