I

在 $\triangle$ABC 中，M 為 $\overline{BC}$ 邊之中點，若 $\overline{AB}$ = 3， $\overline{AC}$ = 5，且 $\angle$BAC = 120^o ， 則 tan$\angle$BAM 之值為何?

說明:由此次的考題整體來看, 這一題可能要考三角測量. 前面好幾題坐標平面的問題都可以用幾何的方式處理而不需設坐標. 此題雖未提坐標平面, 卻可用坐標處理. 不過若用坐標, 可能就和三角測量中的那些正弦餘弦定理沒什麼關係了.

若用三角函數的性質直接在題目中的三角形處理, 好像不容易, 需畫輔助線簡化問題. 不過在筆者可想的各種方法中, 看不出出題者特別問``tan''函數的用意何在. 反倒是 tangent 函數讓人聯想到直線斜率, 這樣就和坐標幾何有關了. 在筆者可想到的方法中, 此題用坐標的方式處理最為簡明. 或許出題者的用意真的是要考幾何的問題坐標化.

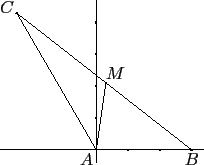
這裡我們就只提供座標化的處理方法. 由於題目問的是有關 $\angle$BAM, 所以我們很自然的會將 A 置於原點, 而 B 點置於 x 軸正向上 (即 B 點坐標為 (3, 0)). 作圖如下:

由於 $\angle$BAC = 120^o 且 $\overline{AC}$ = 5, 我們可得 C 點坐標為 (5 cos 120^o, 5 sin 120^o) = (- 5/2, 5$\sqrt{3}$/2). 因此馬上得 $\overline{BC}$ 的中點 (即 M 點) 坐標為 (1/4, 5$\sqrt{3}$/4). 故得

tan$$\angle$$BAM = $${\frac{\frac{5\sqrt{3}}{4}}{\frac{1}{4}}}$$ = 5$$\sqrt{3}$$.