

下一頁: I
上一頁: 三、選填題
前一頁: G
坐標平面上有一以點 V(0, 3) 為頂點、F(0, 6)
為焦點的拋物線。設 P(a, b) 為此拋物線上一點,Q(a, 0) 為 P 在
x 軸上的投影,滿足
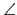 FPQ = 60o,求 b 之值.
FPQ = 60o,求 b 之值.
說明:本題明明白白的就是考拋物線. 可以寫下此拋物線的方程式,
然後坐標幾何的方式求解; 也可以由拋物線的定義, 直接用幾何方式求解.
若用坐標的方式, 由題目給的條件
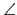 FPQ = 60o,
應可以用內積解決. 意即先寫下
FPQ = 60o,
應可以用內積解決. 意即先寫下
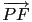 = (- a, 6 - b),
= (- a, 6 - b),
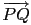 = (0, - b), 再利用此二向量之內積
= (0, - b), 再利用此二向量之內積
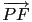 .
. 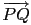 =
= 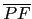
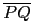 cos 60o 得
cos 60o 得
最後由於 (a, b) 所在拋物線方程式為
x2 = 12(y - 3), 利用
a2 = 12b - 36, 代入上式 (96.5) 解得 b = 0 或 b = 12. 由於 b = 0
不合, 故知 b = 12.
其實關於圓錐曲線的問題很多都可以利用這些曲線的定義來求解.
用定義方式處理的好處是不需特別寫下曲線的方程式
(若曲線經過旋轉就不容易寫下方程式). 首先大致作圖如下.
要注意雖然我們將 P 點標於第一象限, 但因為我們是用幾何的方法, 所以這裡 P 點在第一或第二象限都沒有關係.
由於 x 軸是準線, 依拋物線的定義, 我們知
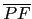 =
=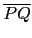 ,
也就是說三角形 FPQ 是一個等腰三角形. 又知
,
也就是說三角形 FPQ 是一個等腰三角形. 又知
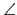 FPQ = 60o,
故得三角形 FPQ 事實上是一個正三角形. 因此, 若令 O 為原點,
則三角形 FQO 為直角三角型且
FPQ = 60o,
故得三角形 FPQ 事實上是一個正三角形. 因此, 若令 O 為原點,
則三角形 FQO 為直角三角型且
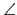 FQO = 30o. 所以由
FQO = 30o. 所以由
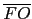 = 6, 得知
= 6, 得知
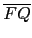 =
= 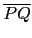 = 12, 即 b = 12.
= 12, 即 b = 12.
當然了, 數學方法中並沒有說一次只能用一種方法處理問題.
有時各種方法互相配合使用, 也是不錯的選擇. 例如此題, 若用坐標的方法,
又利用幾何性質知道了
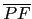 =
= 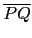 . 那麼在式子 (96.5)
中就可以直接由
a2 + (6 - b)2 = b2, 而求得 b 之值了.
. 那麼在式子 (96.5)
中就可以直接由
a2 + (6 - b)2 = b2, 而求得 b 之值了.
Li
2007-08-02
![]() FPQ = 60o,
應可以用內積解決. 意即先寫下
FPQ = 60o,
應可以用內積解決. 意即先寫下
![]() = (- a, 6 - b),
= (- a, 6 - b),
![]() = (0, - b), 再利用此二向量之內積
= (0, - b), 再利用此二向量之內積
![]() .
. ![]() =
= ![]()
![]() cos 60o 得
cos 60o 得 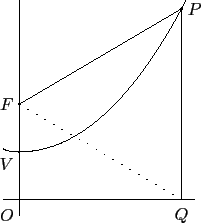
![]() =
= ![]() . 那麼在式子 (96.5)
中就可以直接由
a2 + (6 - b)2 = b2, 而求得 b 之值了.
. 那麼在式子 (96.5)
中就可以直接由
a2 + (6 - b)2 = b2, 而求得 b 之值了.