G

摸彩箱裝有若干編號為 1, 2,..., 10 的彩球，其中各種編號的彩球數目可能不同。今從中隨機摸取 一球，依據所取球的號數給予若干報酬。現有甲、乙兩案：甲案為當摸得彩球的號數為 k 時，其所獲報酬同為 k；乙案為當摸得彩球的號數為 k 時，其所獲報酬為 11 - k ( k = 1, 2,..., 10)。已知 依甲案每摸取一球的期望值為 67/14，則依乙案每摸取一球的期望值為何?

說明:這一題考的就是期望值. 要了解到期望值的定義還有機率上所有事件發生的機率為 1. 題目中沒有給出取出每一編號的機率, 所以要善用未知數大膽的先去假設取出 k 號球的機率為 p_k, 再用期望值的定義去處理. 要注意題目沒有給 p_k 值, 並不表示可以隨便設定 p_k 值. 這些 p_k 是有限制的, 題目中給的甲案每摸取一球的期望值就是限制這些 p_k. 當然了若你能找到一組 p₁,..., p₁₀ 使得依甲案每摸取一球的期望值為 67/14, 那麼就可以利用這一組 p_k 值求得乙案的期望值. 不過很明顯的, 出題者不是要我們這樣做.

依期望值的定義甲, 乙兩案的期望分別為

p₁ + 2p₂ + ^... 9p₉ + 10p₁₀,    (11 - 1)p₁ + (11 - 2)p₂ + ^... (11 - 9)p₉ + (11 - 10)p₁₀.

若同學有衝動將乙案的期望值寫成

10p₁ + 9p₂ + ^... + 2p₉ + p₁₀,

很可能就做不下去了 (除非很幸運地看到甲乙兩案期望值之和為 11(p₁ + p₂ ^... + p₉ + p₁₀)). 不過若同學習慣用 summation 的符號, 那麼甲, 乙兩案的期望分別為

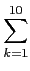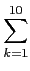
$$\sum_{k=1}^{10}$$kp_k,    $$\sum_{k=1}^{10}$$(11 - k)p_k.

將乙案的期望值整理一下就可得

11$$\sum_{k=1}^{10}$$p_k - $$\sum_{k=1}^{10}$$kp_k = 11 - $$\sum_{k=1}^{10}$$kp_k,

很快就得到兩個期望值之間的關係了. 從這裡可看出, 具體的數字沒錯很好操作, 但有時多餘的計算會讓我們看不出問題的形式. 這也是為什麼我們處理數學問題時常用一般的未知數來處理, 它能讓我們了解這個問題的基本形式, 且能將問題推廣到更一般的狀況.