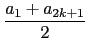D

某巨蛋球場 E 區共有 25 排座位，此區每一排都比其前一排多 2 個座位。小明坐在正中間那一排(即第 13 排)，發現此排共有 64 個座位，則此球場 E 區共有幾個座位。

說明:此題只考等差級數, 頂多可以說還要考同學是否能將此情境換成數學模式來處理. 不過或許是為了情境上好處理, 題目上明白寫出此等差數列的公差為 2, 這就浪費了小明剛好坐在最中間那一排的好處了. 同學們可能會由公差以及項數求出第一排的座位數, 再利用等差級數的公式求出所有座位數. 事實上因為此等差數列有奇數項又知道最中間項的值, 不管公差是多少此數列之和就確定了 (注意是級數和可以確定並不是指此數列可以確定). 這是因為若 a₁,..., a_{2k + 1} 是一個有 2k + 1 項的等差數列, 則最中間一項 (即 a_{k + 1}) 會是首項和末項的算術平均, 即

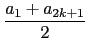$${\frac{a_1+a_{2k+1}}{2}}$$ = a_{k + 1}.

故得級數和為

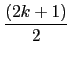$${\frac{(2k+1)}{2}}$$(a₁ + a_{2k + 1}) = (2k + 1)(a_{k + 1}).

因此不管公差是多少, 此題答案皆為 25×64 = 1600.