

下一頁: 6
上一頁: 二、多選題
前一頁: 二、多選題
下面每一個選項都是以行列式表達坐標平面上的方程式,
請問哪些選項代表橢圓?
說明:此題應該是有關兩個不同的概念, 一個是行列式的求值問題,
另一個是橢圓方程式. 若對線性代數熟悉的話都了解行列式為 0
應和向量線性相依有關, 此題考的是二次曲線應和向量無關,
所以應該沒有什麼快的方法將此兩個概念一次連結, 只好分兩步驟處理.
第一步就是化簡行列式. 看到五個行列式要去計算難免頭大,
不過仔細看看發現每個矩陣下面兩列(橫向)皆相同.
看來出題者希望同學用降階的方式處理 3×3 行列式, 也就是
如果不會降階, 直接用斜對角方式計算也可得上面式子.
再將 r, s, t 代每個選項所對應的位置的多項式, 就可得到五個方程式.
第二步就屬於知識性的問題, 由前面算出的五個方程式看出都沒有 xy 項,
所以題目所指的橢圓應該都是未經旋轉的,
也就是說都是標準式再經平移就可得. 這樣的橢圓方程式皆有以下的形式:
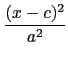
+
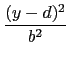
= 1.
所以若展成
Ax2 + By2 + Cx + Dy + E = 0 的形式, A 和 B 皆不等於 0
且相異但同號(即同正同負), 因此可以看出只有選項 (2) 和 (3) 是可能的.
或許出題者好心認為同學做到這裡已不錯了, 所以沒有搞鬼(考退化的情形).
要注意即使 A, B 同號未必就是橢圓, 有可能是退化成一點或空集合.
考試時還是要小心確認配方後可化成
A(x - c)2 + B(y - d )2 = F, 其中 F
不為 0 且與 A, B 同號才是橢圓. 其實快一點的方法可由行列式知
(x, y) = (0, 0) 皆滿足這五個式子 (即其圖形皆通過原點)
所以不可能退化成空集合, 又如果退化成一點則必退化成原點,
即其方程式應為
Ax2 + By2 = 0 (A, B 同號) 所以選項 (2) 和 (3)
也不可能退化成一點. 不過這樣的看法不是通則,
一般情形還是規規矩矩用配方法處理較保險.
Li
2007-08-02
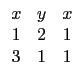
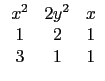
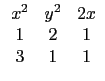
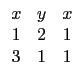
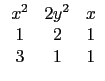
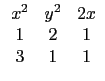
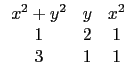
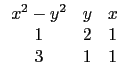
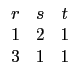
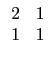
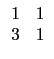
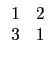
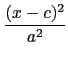 +
+ 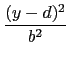 = 1.
= 1.