冠軍
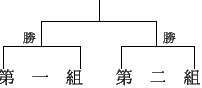

說明:此題可能為了避免條件機率而假設各隊獲勝的機率均等.
如此一來不管如何分組, 由於每一種賽程表發生的機會均等,
所以可以用古典機率來求其機率.
也就是說我們只要用排列組合的方法算出所有可能的賽程表個數以及由甲乙兩隊做冠亞軍對戰的賽程表個數就可得其機率.
近幾年的排列組合問題, 由於數字不大, 幾乎都可以用直接列出的方式求解. 當然這樣不是萬無一失的, 數字大了就麻煩了, 所以我們總是希望能用學過的排列組合的方法解決. 這樣又牽扯到一個問題就是往往可以有很多種看法處理. 有的看法很有效率一下子就正確無誤的把問題解決; 有的看法很複雜又常出錯(多算或少算). 確實排列組合的問題沒有一定的法則說哪種看法最有效率, 所以在思考時可能儘量用各種看法試試看, 若想不到太多的看法也沒關係, 最重要的是注意有沒有多算或少算.
這裡提供一個可能的錯誤看法:「由於各隊要先抽被分到哪一組, 因為僅有二組, 所以每隊抽到的組別共有兩種可能. 因為共有四隊, 所以用乘法原理知共有 24 種可能. 接著看每一種分組情況每組各有兩隊, 這兩隊皆有可能獲勝, 所以每一組有兩種可能. 因為有兩組所以在用乘法原理知每一種分組情況共可能產生 22 種賽程. 由於共有 24 種分組情況而每一種分組情況共可能產生 22 種賽程, 因此再依乘法原理知共可能有 24×22 = 26 種賽程.」這一個看法共用了三次的乘法原理, 不過第一個用錯了. 沒錯, 每一隊所抽到的組別共有兩種可能, 不過這樣的看法並沒有考慮到每一組僅能有兩隊的限制. 也就是說這個乘法原理所得的結果多算了很多不正確的情形, 即一組有 3 隊另一組有 1 隊以及一組有 4 隊另一組有 0 隊的情形. 知道多算了同學可以考慮換別種看法, 或是把多算的情形扣掉. 多算了哪些呢? 3 隊在第一組 1 隊在第二組的情形共有 4 種, 即甲、乙、丙、丁分別在第二組這四種. 同理 3 隊在第二組 1 隊在第一組的情形共有 4 種. 另外 4 隊在第一組 0 隊在第二組的情形只有 1 種. 再加上 4 隊在第二組 0 隊在第一組的 1 種情形, 共有 4 + 4 + 1 + 1 = 10 種情形需扣除. 所以最後算得共有 24 - 10 = 6 種分組情況. 另一種分組的看法是從組來挑隊伍, 這樣才能確實掌握每組只能有兩隊的狀況. 所以由第一組挑兩隊共有 C24 = 6 種選法, 而剩餘兩對自動歸於第二組, 所以第一組挑完後第二組只有 1 種情況, 因此依乘法原理知共有 6 種分組情況, 再依乘法原理知共有 6×4 = 24 種賽程. 算出了所有可能賽程個數後, 還需算甲乙兩隊爭冠軍的賽程個數. 很容易理解甲乙要爭冠軍就不能分到同一組. 所以會有同學認為可以有甲在第一組乙在第二組和乙在第一組甲在第二組兩種情況. 這樣的看法又少算了, 因為甲在第一組又有丙或丁也在第一組這兩種情況. 所以要讓甲乙兩隊爭冠軍可能的分組有 4 種. 然而每一分組情形要讓甲乙爭冠軍就非得兩隊在該組中勝出, 所以每一分組僅可能產生 1 種賽程使得甲乙爭冠. 因此再用乘法原理知甲乙爭冠的賽程共有 4 種. 最後得機率為 4/24 = 1/6. 在這裡介紹的看法中大家或許能體會由組選隊伍的看法較有效率.
這一題當然也可直接用機率的看法處理. 用機率的看法好處是即使各隊的勝率不同也可處理. 機率的算法大致上是先算出甲乙兩隊被分到不同組的機率再乘上所對應的勝率. 同樣的用機率也可有很多種看法, 依然要注意有沒有多算少算的情形. 這裡再提供一個可能的錯誤看法:「由於只有兩組, 甲隊被分到第一組的機率為 1/2, 同理乙隊被分到第二組的機率是 1/2, 所以甲乙分別被分到一二兩組的機率為 1/4. 同理, 乙甲分別被分到一二兩組的機率為 1/4. 故得甲乙二隊被分到不同組的機率為 1/4 + 1/4 = 1/2. 由於甲乙被分到不同組後甲乙分別勝出的機率各為 1/2, 所以甲乙同時勝出的機率為 (1/2)×(1/2) = 1/4. 最後得甲乙爭冠軍的機率為 (1/2)×(1/4) = 1/8.」如同前面排列組合的方法, 這個看法錯在一開始算甲乙被分到不同組的機率. 這個看法類似於前面所提由甲乙丙丁四隊選組的看法, 不過其錯誤的原因不只有如前面發生一組可能有多於兩隊的可能, 而且甲隊選第一組和乙隊選第二組兩事件並不獨立沒有道理機率乘在一起. 這個錯誤看法較難修正我們就不去處理了. 讓我們再看一種求甲乙不同組的機率的錯誤看法:「第一組選甲隊的機率為 1/4 (因為有四隊), 再從剩下三隊選丙丁兩隊 (因甲乙不能同組) 的機率為 2/3, 所以甲隊在第一組且乙隊在第二組的機率為 (1/4)×(2/3) = 1/6. 同理甲隊在第二組且乙隊在第一組的機率為 1/6, 故得甲乙二隊在不同組的機率為 1/6 + 1/6 = 1/3.」這一種看法如同前面排列組合由兩組選隊伍的看法克服了一組需僅有兩隊的困難, 而且條件機率的看法也沒有錯誤, 看起來好像沒有問題, 不過仍少算了一些情形. 因為第一組要選兩個隊伍時並沒有順序之分, 而這裡在算甲隊在第一組且乙隊在第二組的機率時錯誤的地方是僅考慮先選甲隊再選丙或丁的情況, 而沒有考慮先選丙或丁再選甲隊的情況. 由於先選丙或丁的機率為四隊中選兩隊其機率為 2/4 = 1/2, 而選好後再選甲隊的機率為剩下的三隊選一隊, 其機率為 1/3, 因此知先選丙或丁再選甲隊的機率為 (1/2)×(1/3) = 1/6. 所以甲隊在第一組且乙隊在第二組的機率應該是前面所算的 1/6 加上這裡少算的 1/6 為 1/3. 同理甲隊在第二組且乙隊在第一組的機率為 1/3, 故得甲乙二隊在不同組的機率為 1/3 + 1/3 = 2/3. 其實這裡考慮分組情況的機率每種情況發生的機會均等, 可以用排列組合來處理. 也就是因為共有 6 種分組法而其中甲乙在不同組的分法有 4 種, 所以得甲乙二隊在不同組的機率為 4/6 = 2/3. 有時在處理機率問題時適時的運用排列組合的觀點也是不錯的選擇. 此題用機率的方法處理的最後一步就是甲乙在不同組後同時勝出的機率為 (1/2)×(1/2) (因為獨立事件), 所以由條件機率的看法知甲乙爭冠軍的機率為甲乙二隊在不同組的機率乘上甲乙同時勝出的機率, 即 (2/3)×(1/4) = 1/6. 最後提醒一下由於此題各隊勝率皆相同, 所以我們處理時直接先算甲乙二隊在不同組的機率. 一般情形應該是先算出甲乙二隊在不同組所有情況的機率 (如甲丙在一組, 乙丁在另一組的機率為 1/6) 再乘上其對應的勝率 (如甲丙一組, 乙丁在另一組, 則需分別乘上甲勝丙的機率以及乙勝丁的機率), 然後再將所有情況所得機率都加起來.