一

某別墅有一個由四塊正方形的玻璃拼成的田字形窗戶， 窗外路燈的光線( 假設路燈是一個點光源)透過窗戶在地板上形成一個變形的田字形光影。 在地板上建置一個直角坐標系， 發現田字形光影外框的四個頂點的坐標分別為 (- 4, 40), (16, 0), (16, 40) 和 (28, 16) 。求田字形窗戶的中心投影在地板上的坐標。

說明:由題目僅給四點求中心點的投影來看, 此題出題者想考的是直線的投影仍是直線這樣的概念以及坐標平面上的直線方程式. 雖然直線的投影仍是直線這樣的概念算是蠻直觀的數學概念, 但是如何運用在處理這個問題上對一般同學確實是很困難的問題. 尤其在高中數學課程中常見用投影概念來處理問題, 並沒有一個專門的章節處理投影本身的性質, 在考場上碰到這樣的問題確實棘手.

讓我們從題目本身出發看看如何處理這個問題. 題目給了幾個已知的條件是:

(1) 窗戶是由四塊正方形玻璃拼成的田字形窗戶. 從田字形這個提示大家應覺得此四塊正方形皆相同. 既然相同的四個正方形拼成的, 所以此窗戶依然是正方形;

(2) 此正方形窗戶的四個頂點的投影坐標.

既然只有這兩條件, 要如何從這兩條件得到中心點的投影坐標呢? 假設原正方形的頂點分別為 A, B, C, D 而其投影分別為 A', B', C', D'. 由於窗戶中心的投影來自於窗戶中心, 所以我們需思考如何由 A, B, C, D 四點得到窗戶的中心. 我們有兩種看法. 第一種是這中心是正方形兩對角線 (即線段 $\overline{AC}$ 和 $\overline{BD}$) 的交點; 另一種是兩對邊中點連線 (即 $\overline{AD}$ 和 $\overline{BC}$ 的中點連線以及 $\overline{AB}$ 和 $\overline{CD}$ 的中點連線) 的交點.

若是依第一種看法, 由於 $\overline{AC}$ 通過 A, C 兩點, 故 $\overline{AC}$ 的投影必通過 A' 和 C'. 又由於直線的投影仍為直線, 所以 $\overline{AC}$ 的投影就是 $\overline{A'C'}$. 同理 $\overline{BD}$ 的投影就是 $\overline{B'D'}$. 因此既然正方形的中心為 $\overline{AC}$ 和 $\overline{BD}$ 的交點 (即中心在 $\overline{AC}$ 上也在 $\overline{BD}$ 上), 所以中心的投影點也同時在 $\overline{A'C'}$ 和 $\overline{B'D'}$ 上, 即為 $\overline{A'C'}$ 和 $\overline{B'D'}$ 的交點.

若是依第二種看法就慘了. 雖然中心的投影仍為兩對邊中點連線的投影的交點, 但這兩個對邊的中點連線的投影跑到哪裡就不得而知了. 這是因為投影並不保持距離 (與光源距離不同投影長就不同), 所以不見得一個線段的中點其投影仍為此線段的投影線段的中點. 我們就用下圖這個較特殊的情形來說明.

此圖中 C 為 $\overline{AB}$ 的中點. A' 和 C' 分別為 A 和 C 在水平地面的投影, B 的投影仍為 B. 很容易看出 C' 並不是 $\overline{AB}$ 的投影 $\overline{A'B}$ 的中點. 否則直線 CC' 會平行直線 AA' 它們不可能相交於光源.

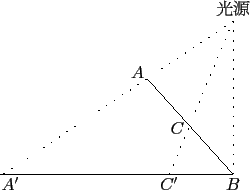
所以此題的作法應是在坐標平面上標出此四投影點, 確認哪兩點互為對角線上的點, 求出其連線的直線方程式, 再求兩直線的交點坐標. 若不作圖, 也可任取一點求其和其他三點的連線斜率, 而確認哪一點可與其成為對角線. 此題有兩點 (16, 0) 和 (16, 40) 的連線為鉛直線, 而 (16, 0) 和其他兩點連線的斜率為一正一負, 所以很快的看出 (16, 0) 和 (16, 40) 的連線是對角線. 或許出題者讓兩投影點的 x 軸坐標相同用意在此.

從此題的解法看出, 題目僅需假設窗戶是矩形即可. 出題者將窗戶設計成由四塊相同的正方形拼成的田字形窗戶, 不知是否有意無意的要誤導同學用錯誤的第二種看法 (即求兩對邊中點連線的交點). (這個多餘的條件和單選題第一題不足的條件, 形成一個有趣的對比.) 有些人質疑正方形的投影是否可能形成如題所述的等腰梯形, 本人倒不在意. 反而覺得大家應該探討的是我們真的需要``設計''一個題目到 訓練高中生在短暫的考試中面對一個完全不熟悉的概念時, 仍能嚴謹的辨識出錯誤的概念嗎?