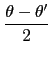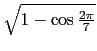
(1)
2 sin![]() (2)
sin
(2)
sin![]() (3)
(3)
![]() sin
sin![]() (4)
(4)
![]() (1 - cos
(1 - cos![]() ) (5)
) (5)
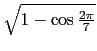
說明:這一題考的是複數的絕對值, 順便考一下三角函數的半角公式.
不過若能知道 z 和 1 都在複數平面上以原點為原心的單位圓上,
就能用較幾何的方法處理而避開半角公式.
用直關比較代數的方法處理, 我們馬上有
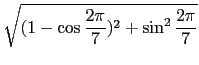 =
= 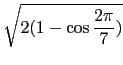
我們可以發現這個問題和角度是無關的, 也就是說若
0![]()
![]()
![]()
![]() 且
z = cos 2
且
z = cos 2![]() + i sin 2
+ i sin 2![]() , 則
, 則
![]() 1 - z
1 - z![]() = 2 sin
= 2 sin![]() .
這是巧合嗎? 還是有什麼特殊原因呢? 我們曾經碰到類似的情況,
就是用代數的方法, 有些性質會在等式運算中被掩蓋了而無法看出,
但若用幾何的看法就可很清楚的知道其原因.
.
這是巧合嗎? 還是有什麼特殊原因呢? 我們曾經碰到類似的情況,
就是用代數的方法, 有些性質會在等式運算中被掩蓋了而無法看出,
但若用幾何的看法就可很清楚的知道其原因.
假設
0![]()
![]()
![]()
![]() 且
z = cos 2
且
z = cos 2![]() + i sin 2
+ i sin 2![]() .
將複數置於複數平面上, 此時兩複數 w, w' 之差的絕對值, 即
.
將複數置於複數平面上, 此時兩複數 w, w' 之差的絕對值, 即
![]() w - w'
w - w'![]() 會等於 w 和 w' 在複數平面上所對應的點之間的距離.
由於
會等於 w 和 w' 在複數平面上所對應的點之間的距離.
由於
![]() z
z![]() =
= ![]() 1
1![]() = 1, 我們知 z 和 1 都落在以 0
為圓心半徑為 1 的單位圓上. 若我們將單位圓繞著圓心順時鐘轉
= 1, 我們知 z 和 1 都落在以 0
為圓心半徑為 1 的單位圓上. 若我們將單位圓繞著圓心順時鐘轉 ![]() 角, 則 z 點會被轉到
cos
角, 則 z 點會被轉到
cos![]() + i sin
+ i sin![]() 的位置, 而 1
會被轉到
cos(-
的位置, 而 1
會被轉到
cos(- ![]() ) + i sin(-
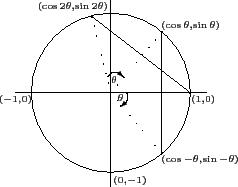
) + i sin(- ![]() ) 的位置, 如下圖.
由於我們只是將單位圓旋轉, 兩點經旋轉後距離不變. 所以 1 和 z
之間的距離等於
cos
) 的位置, 如下圖.
由於我們只是將單位圓旋轉, 兩點經旋轉後距離不變. 所以 1 和 z
之間的距離等於
cos![]() + i sin
+ i sin![]() 和
cos(-
和
cos(- ![]() ) + i sin(-
) + i sin(- ![]() ) 之間的距離, 故得
) 之間的距離, 故得
![]() 1 - z
1 - z![]() = 2 sin
= 2 sin![]() .
.
當然了代數觀點和幾何觀點可合併處理. 若
z = cos 2![]() + i sin 2
+ i sin 2![]() ,
令
w = cos
,
令
w = cos![]() + i sin
+ i sin![]() . 則因
. 則因
![]() w
w![]() = 1, 可得
= 1, 可得
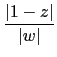 =
=