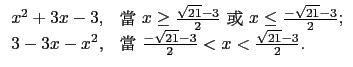
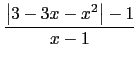 的敘述何者正確?
的敘述何者正確?
(1) 極限不存在 (2) 極限為 0 (3) 極限為 1 (4) 極限為 5 (5) 極限為 -2
說明:此題是希望了解絕對值取值問題, 再將函數化成分式求其極限.
這類問題同學們大多會處理, 我們僅想利用這個機會再澄清一些極限概念.
處理此題, 應先處理絕對值部份, 希望能將分子化成多項式, 這樣就能處理分式. 或許同學會規規矩矩寫下
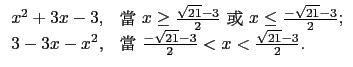
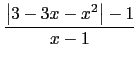 =
= 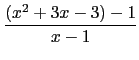
下一步就要處理極限了. 一般同學處理極限會先代值看看,
若可取值那就是極限值; 若不能取值 (如分母為 0) 再另行處理.
這樣的方式和正確的極限觀念是有出入的
(造成很多同學誤以為此題極限不存在), 這是因為依定義
![]() f (x) 是指當 x 越來越靠近 a 時 f (x) 所越來越靠近的值,
基本上和 f (x) 在 x = a 的取值是無關的. 但如果 f (x) 是連續函數,
表示當 x
越來越靠近 a 時 f (x)
越來越靠近 f (a), 所以 f (x) 在 x 趨近於 a 的極限值就是
f (a). 這裡要強調是, 要先確定函數是在求極限的點是連續的, 再代值.
本題接下來的處理方式, 很多同學會寫下
f (x) 是指當 x 越來越靠近 a 時 f (x) 所越來越靠近的值,
基本上和 f (x) 在 x = a 的取值是無關的. 但如果 f (x) 是連續函數,
表示當 x
越來越靠近 a 時 f (x)
越來越靠近 f (a), 所以 f (x) 在 x 趨近於 a 的極限值就是
f (a). 這裡要強調是, 要先確定函數是在求極限的點是連續的, 再代值.
本題接下來的處理方式, 很多同學會寫下
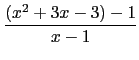 =
= 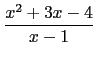 = x + 4
= x + 4
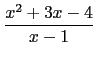 =
= 由於這題是選擇題, 同學不需寫下這麼標準的式子. 我們特別這樣寫下來, 是希望同學了解求極限的問題, 最大的原則是將要求的函數表為在求極限點附近的連續函數再代值, 而不是一開始不管怎樣就先代值.