(1) 圖形有最高點,也有最低點 (2) 圖形有水平切線
(3) 圖形與任一水平直線恰有一交點
(4) 若 (a, b) 在圖形上, 則 (- a, - b + 6) 也在圖形上
(5) 圖形與三直線 x = 0, x = 1, y = 0 所圍成的區域之面積大於 4
說明:本題問的是三次多項式函數的圖形,
比較著重於一次導函數和函數圖形切線斜率的關係(即陡峭情形).
我們僅討論和一次導函數相關的選項. 因為
f (x) = x3 + 2x + 3
的一次導函數為
f'(x) = 3x2 + 2, 對任意實數 x, 皆有
f'(x)![]() 2,
所以此圖形不會有水平切線. 由於 f'(x) > 0, 知此函數一直是遞增,
即其圖形一直上升, 所以任一水平直線與之最多有一交點. 但由選項 (1)
可知此函數當 x 趨近於正無限大和負無限大時,
其取值分別趨近於正無限大和負無限大, 故此函數對所有的實數皆可取值.
因此知此函數圖形與任一水平直線恰有一交點.
2,
所以此圖形不會有水平切線. 由於 f'(x) > 0, 知此函數一直是遞增,
即其圖形一直上升, 所以任一水平直線與之最多有一交點. 但由選項 (1)
可知此函數當 x 趨近於正無限大和負無限大時,
其取值分別趨近於正無限大和負無限大, 故此函數對所有的實數皆可取值.
因此知此函數圖形與任一水平直線恰有一交點.
最後一個選項較為棘手, 我們需了解此函數圖形在 x ![]() [0, 1]
間的成長情形. 當 x = 0 時函數取值為 f (0) = 3 此時其切線斜率為
f'(0) = 2. 但當 x > 0 時, 其切線斜率
f'(x) = 3x2 + 2 皆大於 2,
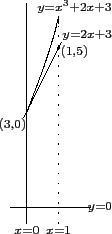
也就是說 y = f (x) 在 x = 0 的切線方程式為 y = 2x + 3, 但當 x > 0
時由於 y = f (x) 都以比 y = 2x + 3 更陡的方式爬升, 所以此時 y = f (x)
的圖形皆在 y = 2x + 3 圖形的上方. 如下圖.
[0, 1]
間的成長情形. 當 x = 0 時函數取值為 f (0) = 3 此時其切線斜率為
f'(0) = 2. 但當 x > 0 時, 其切線斜率
f'(x) = 3x2 + 2 皆大於 2,
也就是說 y = f (x) 在 x = 0 的切線方程式為 y = 2x + 3, 但當 x > 0
時由於 y = f (x) 都以比 y = 2x + 3 更陡的方式爬升, 所以此時 y = f (x)
的圖形皆在 y = 2x + 3 圖形的上方. 如下圖.