6

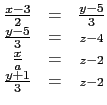
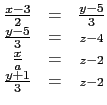
$\displaystyle \left\{\vphantom{ \begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3}... ...iptstyle{z-2} \\ \frac{y+1}{3} &=& \scriptstyle{z-2} \end{matrix}%% }\right.$ $\displaystyle \begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3} \\ \frac{y-5}{... ...a} &=& \scriptstyle{z-2} \\ \frac{y+1}{3} &=& \scriptstyle{z-2} \end{matrix}$

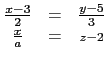(3) 方程組 $\left\{\vphantom{ \begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3} \\ \frac{x}{a} &=& \scriptstyle{z-2} \end{matrix}%% }\right.$ $\begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3} \\ \frac{x}{a} &=& \scriptstyle{z-2} \end{matrix}$ 有無窮多解 (4) 方程組 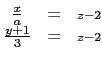$\left\{\vphantom{ \begin{matrix} \frac{x}{a} &=& \scriptstyle{z-2} \\ \frac{y+1}{3} &=&\scriptstyle{z-2} \end{matrix}%% }\right.$ $\begin{matrix} \frac{x}{a} &=& \scriptstyle{z-2} \\ \frac{y+1}{3} &=&\scriptstyle{z-2} \end{matrix}$ 有唯一解

(5) 方程組 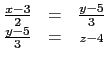$\left\{\vphantom{ \begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3} \\ \frac{y-5}{3} &=& \scriptstyle{z-4} \end{matrix}%% }\right.$ $\begin{matrix} \frac{x-3}{2} &=& \frac{y-5}{3} \\ \frac{y-5}{3} &=& \scriptstyle{z-4} \end{matrix}$ 有無窮多解

說明:本題雖然題目考的是方程組解的問題, 不過由方程組的形式可以看出出題者希望從空間幾何的角度著手. 而且雖然好像問的是四個平面的相交情形, 不過出題者希望從兩直線的相交情形來處理.

為了方便, 我們將題目中的聯立方成組從上到下分別稱為第一式, 第二式, 第三式以及第四式. 若從解方程式的角度處理, 很快的看出第二式和第四式是一樣的, 所以問題本質上還是處理三個式子的聯立方程式, 所以還是可以利用一般判別聯立方程式解的情況的方式處理. 不過由於用空間幾何的方法確有其方便性, 這裡我們就順著出題者的意思, 用處理兩直線相交情形的方式進行. 利用大家熟悉的空間中直線的比例式, 我們可看出第一式和第二式所代表的是通過 (3, 5, 4) 且方向向量為 (2, 3, 1) 的直線, 而第三式和第四式所代表的是通過 (0, - 1, 2) 且方向向量為 (a, 3, 1) 的直線. 依這種觀點我們可以回答選項 (1) 和 (2). 若 a = 2 表示這兩直線的方向向量平行, 此時有解 (即有交點) 的意思是它們為同一直線. 有就是說 (3, 5, 4) 和 (0, - 1, 2) 這兩點都在此直線上, 但由此兩點所決定的向量是 (3, 5, 4) - (0, - 1, 2) = (3, 6, 2) 和直線的方向向量 (2, 3, 1) 並不平行, 由此矛盾知 a $\ne$ 2. 既然 a $\ne$ 2, 表示此二直線不平行, 但它們又不歪斜 (因已知有交點), 故知必相交於一點. 因此知原方程式有唯一解. 選項 (3), (4), (5) 其實問的都是兩平面的相交情形, 可以由它們的法向量都不平行知皆有無窮多解.

若依原題, 選項 (1) 有點奇怪而且``浪費''了第二式和第四式是同一平面的事實. 此題若一開始原方程組假設是無解, 那麼選項 (1) 就很有意思 (不過這就得犧牲選項 (2)). 因為無解的情形只有兩直線互相平行或歪斜. 但第二式和第四式是同一平面, 表示由一、二式和三、四式所決定的兩直線是落於同一平面上, 所以此二直線不可能歪斜. 由此知若方程組無解, 唯一的可能就是兩直線互相平行, 即 a = 2. 此時此二直線確實平行. 故知方程組無解若且唯若 a = 2.