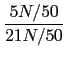A

某公司共有 6 個工廠，各工廠的產量都一樣，且所生產的產品都放進同一倉庫 中。由過去的經驗知道，第 k 個工廠的產品不良率為 ${\dfrac{k}{50}}$ ，其中 k = 1, 2, 3, 4, 5, 6，為了檢驗倉庫中這一批產品的品質， 從倉庫中任意抽出一件，若為不良品， 則此不良品是來自第五個工廠的機率為何？

說明:這一題考的是機率. 由於每個產品被抽取到的機會皆相同, 此題可直接從古典機率的觀點處理. 比較會出錯的地方是, 同學們沒有弄清題意, 而處理和題意不同的事件的機率.

同學或許會認為抽到第五個工廠產品的機率為 1/6, 而第五個工廠的不良率為 5/50, 故得機率為 (1/6)×(5/50) = 1/60. 這是錯誤的, 因為這樣算出的機率其實是從所有產品中抽到一個不良品且此不良品是來自第五個工廠的機率. 而題目問的是若已知抽出的是不良品, 則此不良品是來自第五個工廠的機率. 用白話一點的說法, 題目問的是從所有的不良品中抽到第五個工廠所生產的機率. 兩個事件雖然問的都是抽到第五個工廠生產的不良品, 但一個是從所有的產品中抽出; 另一個是從所有的不良品中抽出, 這兩個機率當然不同.

由於每個產品被抽取到的機會皆相同, 我們可直接從古典機率的觀點處理. 這樣的方法只要弄清楚問的是從哪個集合中抽出哪個子集合元素的機率, 就可處理. 也就是說若 B 是 A 的子集合, 那麼從 A 之中抽出 B 的元素的機率為 n(B)/n(A) (這裡 n(A), n(B) 分別表示 A, B 的元素個數). 這個題目雖告訴我們每個工廠的產量相同, 但沒有告訴我們產量多少. 不過我們可大膽假設每個工廠生產的產品個數為 N, 因為問的是機率, 最後所得的結果會與 N 無關. 經此假設我們知倉庫中產品總數為 6N, 而 1 到 6 廠所生產的不良品個數依次為 N/50, 2N/50, 3N/50, 4N/50, 5N/50 以及 6N/50. 所以倉庫中共有 21N/50 個不良品. 依此我們可以回答許多相關的機率問題. 例如從倉庫中的產品中抽出一個不良品的機率為不良品的個數 21N/50 除以所有產品的個數 6N, 即 7/100. 而從倉庫中的產品中抽出一個不良品且此不良品是來自第五個工廠的機率為 5N/50 除以 6N, 即前面所提的 1/60. 至於題目所問的從所有不良品中抽到來自第五個工廠的不良品機率, 應為

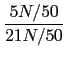$${\frac{5N/50}{21N/50}}$$ = 5/21.