B

在坐標平面上，一圓通過點 (- 2, 7)， 且與直線 4x + 3y - 14 = 0 相切於點 (- 1, 6)，若此圓的方程式為 x² + y² + ax + by + c = 0，則 a, b, c 為何？

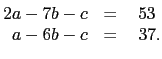
說明:此題考的是與圓相關的概念, 可以用很多種方式處理. 不過若用代數的方法處理, 牽涉到圓的切線公式, 筆者較傾向於幾何的解法. 然而出題者不是直接問圓心與半徑, 用幾何方式處理的同學還要轉換成方程式, 承擔計算錯誤的風險. 看來出題者與筆者意見相左, 較傾向於代數的解法.

代數的方法就是解聯立方程式, 也就是列出 a, b, c 的聯立方程式再求解. 已知 (- 2, 7) 和 (- 1, 6) 滿足 x² + y² + ax + by + c = 0, 依此可得兩個 a, b, c 的三元一次方程式

$$\left\{\vphantom{\begin{matrix}2a-7b-c&=&53\\ \,\,\, a-6b-c&=&\,\,37. \end{matrix}}\right.$$$$\begin{matrix}2a-7b-c&=&53\\ \,\,\, a-6b-c&=&\,\,37. \end{matrix}$$

再利用圓 x² + y² + ax + by + c = 0 在 (- 1, 6) 的切線方程式為 (a - 2)x + (12 + b)y = a - 6b - 2c, 此直線應與 4x + 3y - 14 = 0 相同, 故比較斜率又可得一個 a, b 的二元一次方程式

3a - 4b - 54 = 0.

依此便可解出 a = 10, b = - 6, c = 9.

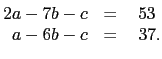
至於利用圓的幾何性質的方法就很多, 最重要的是先找出圓心. 依定義圓心到圓上所有的點的距離皆相等. 因此知 圓心會在 (- 2, 7) 和 (- 1, 6) 這兩點連線的中垂線上, 故得圓心會在直線 x - y + 8 = 0 上. 另外依圓的切線性質, 圓心會在過 (- 1, 6) 且與切線 4x + 3y - 14 = 0 垂直的直線上, 故得圓心會在直線 3x - 4y + 27 = 0 上. 因此兩直線 x - y + 8 = 0 和 3x - 4y + 27 = 0 的交點 (- 5, 3) 就是圓心. 由此可得圓的方程式.

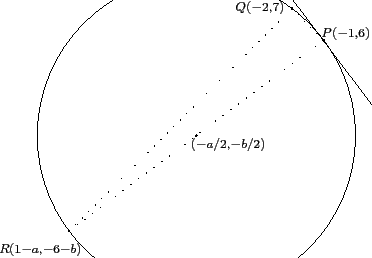
另外也可利用向量的觀點處理. 為了方便, 我們令 P, Q 分別表示 (- 1, 6) 和 (- 2, 7) 這兩點. 依題意, 此圓的圓心坐標為 (- a/2, - b/2), 故與 P(- 1, 6) 在同一直徑的另一端點的坐標為 (1 - a, - 6 - b), 我們用 R 來表示此點, 如下圖.

依圓的切線性質, 向量 $\overrightarrow{PR}$ = (2 - a, - 12 - b) 就是直線 4x + 3y - 14 = 0 的法向量, 故得 3a - 4b - 54 = 0. 另一方面, 利用 直徑所對圓周角為 90^o 的性質, 可知向量 $\overrightarrow{QP}$ = (1, - 1) 與向量 $\overrightarrow{QR}$ = (3 - a, - 13 - b) 垂直, 故得 a - b - 16 = 0. 因此解得 a = 10, b = - 6.