
下一頁: 二
上一頁: 四、非選擇題
前一頁: 四、非選擇題
設
f (x) = x3 - 6x2 - x + 30, 且 a, b 是方程式 f (x) = 0
的兩正根。
(1) 求解三次方程式 f (x) = 0。
(2) 若
 ABC 中,
ABC 中,
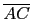 = a,
= a,
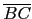 = b,
= b,
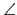 ACB = 120o,且 D, E 是
ACB = 120o,且 D, E 是
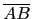 上兩點,滿足
上兩點,滿足
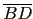 =
= 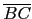 ,
,
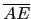 =
= 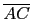 ,試求
,試求
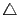 CDE
的面積。
CDE
的面積。
說明:這一題考兩個部份, 一個是解三次多項式方程式,
另一個是考三角測量的問題. 雖然需用第一小題的數據處理第二小題,
但是本質上這是兩個不同的題目, 硬用這種方式將它們連結,
對會處理第二小題但第一小題粗心做錯的同學較吃虧.
第一小題是首項係數為 1 的整係數方程式, 若有有理根必為整數根,
再依提示有兩正根以及根與係數關係很容易得到三個根為 -2, 3, 5.
第二小題解法很多, 首先注意由於兩正根不相同, 所以這裡 a 和 b
會有兩種可能, 但不管是取 a = 3, b = 5 或 a = 5, b = 3
只是將三角形的標示交換而已, 並不影響結果, 所以我們僅討論 a = 3, b = 5
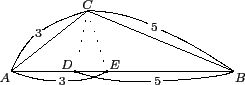
的情形. 首先大致畫個圖形.
注意 D, E 擺放的位置, 需使得
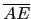 和
和
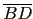 有重疊部分, 這是因為三角形兩邊和大於第三邊.
接下來就是要正式處理此題. 首先不管想用什麼方法都會發現需要知道
有重疊部分, 這是因為三角形兩邊和大於第三邊.
接下來就是要正式處理此題. 首先不管想用什麼方法都會發現需要知道
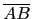 的長度, 馬上利用餘弦定理就可得
的長度, 馬上利用餘弦定理就可得
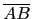 = 7, 由此也知
= 7, 由此也知
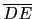 = 1. 下一步處理方法很多, 有的同學心中只知道儘量用正弦,
餘弦定理, 因此想求出其它角或甚至求出
= 1. 下一步處理方法很多, 有的同學心中只知道儘量用正弦,
餘弦定理, 因此想求出其它角或甚至求出
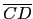 ,
,
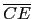 用海龍
(Heron) 公式求
用海龍
(Heron) 公式求
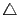 CDE 的面積. 這些方法都可行,
不過大都繞遠路, 或將問題變複雜. 其實這類型的問題雖然解法多,
但若發現處理起來變複雜了, 應適時換個``角度''看問題.
這裡我們舉個較簡明的解法. 由於知道
CDE 的面積. 這些方法都可行,
不過大都繞遠路, 或將問題變複雜. 其實這類型的問題雖然解法多,
但若發現處理起來變複雜了, 應適時換個``角度''看問題.
這裡我們舉個較簡明的解法. 由於知道
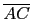 = 3,
= 3,
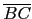 = 5 以及
= 5 以及
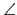 ACB = 120o, 我們可求出
ACB = 120o, 我們可求出
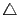 ABC 的面積為
ABC 的面積為
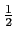
×3×5 sin 120
o =
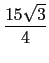
.
這樣的面積算法大都是將
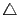 ABC 看成底為
ABC 看成底為
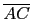 或底為
或底為
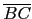 的三角形. 不過也可將
的三角形. 不過也可將
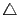 ABC 看成底為
ABC 看成底為
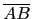 的三角形啊! 如此看法馬上就知
的三角形啊! 如此看法馬上就知
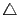 CDE 的面積比上
CDE 的面積比上
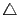 ABC 的面積應為
ABC 的面積應為
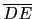 /
/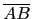 = 1/7, 故得
= 1/7, 故得
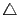 CDE
的面積為
15
CDE
的面積為
15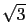 /28.
/28.
Li
2007-08-02
![]() ABC 中,
ABC 中,
![]() = a,
= a,
![]() = b,
= b,
![]() ACB = 120o,且 D, E 是
ACB = 120o,且 D, E 是
![]() 上兩點,滿足
上兩點,滿足
![]() =
= ![]() ,
,
![]() =
= ![]() ,試求
,試求
![]() CDE
的面積。
CDE
的面積。