6

若 $\Gamma$ = {z | z 為複數且 $\left\vert\vphantom{ z-1}\right.$z - 1$\left.\vphantom{ z-1}\right\vert$ = 1}, 則下列哪些點會落在圖形 $\Omega$ = {w | w = iz, z $\in$ $\Gamma$}？

(1) 2i        (2) -2i         (3) 1 + i         (4) 1 - i         (5) -1 + i

說明:此題可能測試同學對集合的認識以及對複數運算和複數的絕對值的了解程度. 雖然題目提示看圖形, 可以很容易利用複數平面的看法作答, 不過若同學對幾何較懼怕的話, 也可用純代數的方法作答.

這裡所謂比較幾何的看法是若將複數對應到坐標平面(即複數平面)上, $\Gamma$ 上的元素是對應到以 (1, 0) 為圓心的單位圓. 由於每個複數乘上 i 相當於將該數所對應的點繞原點逆時鐘轉 90^o, 所以 $\Omega$ 上的元素是對應到以 (0, 1) 為圓心的單位圓. 依此便可判斷哪些點在 $\Omega$ 上. 而所謂代數的方法是將選項中的每個複數 w 除以 i 再驗證是否 w/i 落在 $\Gamma$ 上.

其實不管是用幾何或代數的方法處理此題, 都是用到 $\Omega$ = {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1}. 這裡我們想利用集合的觀點處理. 依題義, $\Gamma$ 中的元素 z 需滿足 $\left\vert\vphantom{ z-1}\right.$z - 1$\left.\vphantom{ z-1}\right\vert$ = 1, 而 $\Omega$ 中的元素和 $\Gamma$ 有關, 而要問哪些元素在 $\Omega$ 中. 既然 $\Omega$ 中的元素和 $\Gamma$ 有關, 而我們又確實了解 $\Gamma$ 中元素的性質, 所以要了解 $\Omega$ 中的元素, 自然是利用 $\Omega$ 和 $\Gamma$ 中元素的關係以及 $\Gamma$ 中元素的性質得到. 任取 $\Omega$ 中的一個元素 w, 依題義 w 是由 $\Gamma$ 中某個元素 z 乘上 i 得到, 也就是說 w = iz. 既然知道 z 的性質, 我們很自然的將 z 寫成 z = w/i 再代入 z 滿足的式子 $\left\vert\vphantom{ z-1}\right.$z - 1$\left.\vphantom{ z-1}\right\vert$ = 1 來得到 w 所要滿足的式子, 即

1 = $$\left\vert\vphantom{ z-1}\right.$$z - 1$$\left.\vphantom{ z-1}\right\vert$$ = $$\left\vert\vphantom{\frac{w}{i}-1}\right.$$$${\frac{w}{i}}$$ - 1$$\left.\vphantom{\frac{w}{i}-1}\right\vert$$ = $$\left\vert\vphantom{\frac{w-i}{i}}\right.$$$${\frac{w-i}{i}}$$$$\left.\vphantom{\frac{w-i}{i}}\right\vert$$ = $${\frac{\left\vert w-i\right\vert }{\left\vert i\right\vert }}$$ = $$\left\vert\vphantom{ w-i}\right.$$w - i$$\left.\vphantom{ w-i}\right\vert$$.

上式的計算中我們用到了基本複數的運算以及複數絕對值的性質. 由上式我們知 $\Omega$ 中任意的元素 w 皆需符合 $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1. 用集合的觀點來看, 我們得到 $\Omega$ 包含於 {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1} 這一個集合. 所以若選項中的元素 w 不能滿足 $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1 (如選項 (2) 的 -2i), 則知此 w 不會在 {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1} 這個集合中, 當然也不會落入 $\Omega$ 裡了 (因為 $\Omega$ $\subseteq$ {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1}). 所以到目前為止我們只知能剔除選項 (2), (4). 其他的選項雖然都符合 {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1}, 但不表示會落在 $\Omega$ 中, 除非我們可以得到滿足 $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1 的 w 會落在 $\Omega$ 中 (即 {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1} $\subseteq$ $\Omega$). 然而如果 w 滿足 $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1. 若將 w 寫成 w = iz, 則

1 = $$\left\vert\vphantom{ w-i}\right.$$w - i$$\left.\vphantom{ w-i}\right\vert$$ = $$\left\vert\vphantom{ iz-i}\right.$$iz - i$$\left.\vphantom{ iz-i}\right\vert$$ = $$\left\vert\vphantom{ i}\right.$$i$$\left.\vphantom{ i}\right\vert$$$$\left\vert\vphantom{ z-1}\right.$$z - 1$$\left.\vphantom{ z-1}\right\vert$$ = $$\left\vert\vphantom{ z-1}\right.$$z - 1$$\left.\vphantom{ z-1}\right\vert$$.

故知 z 是 $\Gamma$ 中的元素, 也就是說 w 確實可以寫成某個 $\Gamma$ 中的元素乘上 i, 得 w 確實在 $\Omega$. 由此我們證得滿足 $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1 的 w 皆在 $\Omega$ 中, 所以可保證其他三個選項的元素皆在 $\Omega$ 中.

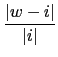上面我們很詳細的證明了 $\Omega$ = {w | $\left\vert\vphantom{ w-i}\right.$w - i$\left.\vphantom{ w-i}\right\vert$ = 1}. 在考試作答時很容易理解此事不需嚴格寫下這麼囉嗦的證明. 我們僅想利用這個證明讓同學們多認識集合. 集合事實上是數學上很方便的符號與工具, 不過有些時候太過抽象, 而較具體的例子(如本題)又可以很直觀的處理, 所以現在大家已對集合概念不作太多的要求了.