
下一頁: 8
上一頁: 二、多選題
前一頁: 6
坐標平面上有相異兩點 P, Q ,其中 P 點坐標為
(s, t)。已知線段
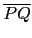 的中垂線 L 的方程式為
3x - 4y = 0,試問下列哪些選項是正確的?
的中垂線 L 的方程式為
3x - 4y = 0,試問下列哪些選項是正確的?
(1) 向量
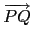 與向量 (3, - 4) 平行 (2) 線段
與向量 (3, - 4) 平行 (2) 線段
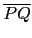 的長度等於
的長度等於
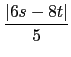
(3) Q 點坐標為 (t, s) (4) 過 Q 點與直線
L 平行之直線必過點 (- s, - t)
(5) 以 O 表示原點,則向量
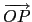 +
+ 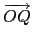 與向量
與向量
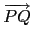 的內積必為 0.
的內積必為 0.
說明:此題應屬有關平面向量的問題. 幾乎所有相關的問題都問了,
考了直線的法向量, 點到線的公式, 平行與對稱的概念, 最後還問了個內積.
這麼多概念都考了對大部分同學來說實屬不易,
更何況出題者充分用到原點在中垂線上這個事實(但此事實卻隱含在題目中),
所以有些選項若用純幾何的觀點還真令人有些吃驚.
此題基本上仍還是有代數(座標幾何)和幾何(平面向量)兩種方式處理.
代數的方法需懂得假設 Q 點坐標, 而幾何的方法便需注意前面所說原點在
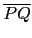 的中垂線上.
的中垂線上.
我們先用代數的方法處理. 選項 (1) 和 (2) 問的是基本的問題,
我們就不多談了. 接下來的選項都和 Q 點有關, 所以我們很大膽的設 Q
點坐標, 看看能否解決問題. 假設 Q 點坐標為 (a, b),
我們要如何利用已知的條件來了解 a 和 b 呢? 要注意雖然 P 點坐標
(s, t) 是以未知的形式出現, 但此處我們要將之看成是已知數,
題目用未知數的方式呈現只是要強調所得的性質對任意的 s, t 皆需成立.
這裡我們唯一的線索是 3x - 4y = 0 是 (s, t) 和 (a, b)
兩點連線段的中垂線, 也就是 3x - 4y 通過 (s, t) 和 (a, b) 的中點
((s + a)/2,(t + b)/2), 而且 3x - 4y = 0 垂直於
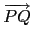 = (a - s, b - t). 由此我們馬上得到下面兩個關係式:
= (a - s, b - t). 由此我們馬上得到下面兩個關係式:
| 3(s + a) |
= |
4(t + b) |
(96.3) |
| 3(b - t) |
= |
-4(a - s) |
(96.4) |
別忘了這裡我們把 s, t 當成已知數, 所以 a 和 b 符合式子
(96.3) 和式子 (96.4) 這一個二元一次聯立方程祖,
我們馬上可解得
a =
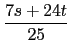
,
b =
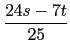
.
其實本題其他選項不必求 a, b 也可以處理. 選項 (3) 雖然談的就是 a, b
之值, 但是若 Q 的坐標為 (t, s), 表示
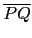 的中點為
((s + t)/2,(s + t)/2), 但是除非 s = t = 0, 這一點不會在 3x - 4y = 0 上,
所以此選項不選. 選項 (4) 問的是 (a, b) 和 (- s, - t) 的連線是否與
3x - 4y = 0 平行, 也就是問向量
(a, b) - (- s, - t) = (a + s, b + t) 是否與向量
(3, - 4) 垂直 (已知選項 (1) 是對的)? 利用由於這兩個向量的內積為
3(a + s) - 4(b + t) 馬上由式子 (96.3) 知道它們是垂直的. 至於選項
(5) 要算的就是向量
(s, t) + (a, b) 與向量 (3, - 4) (已知選項 (1)
是對的)是否垂直? 由於這兩個向量的內積為
3(a + s) - 4(b + t) 再次由式子
(96.3) 知道它們是垂直的. 這裡要注意雖然選項 (4), (5)
我們僅用式子 (96.3) 證明它們是對的, 這並不表示選項 (4), (5)
僅需 3x - 4y = 0 通過
的中點為
((s + t)/2,(s + t)/2), 但是除非 s = t = 0, 這一點不會在 3x - 4y = 0 上,
所以此選項不選. 選項 (4) 問的是 (a, b) 和 (- s, - t) 的連線是否與
3x - 4y = 0 平行, 也就是問向量
(a, b) - (- s, - t) = (a + s, b + t) 是否與向量
(3, - 4) 垂直 (已知選項 (1) 是對的)? 利用由於這兩個向量的內積為
3(a + s) - 4(b + t) 馬上由式子 (96.3) 知道它們是垂直的. 至於選項
(5) 要算的就是向量
(s, t) + (a, b) 與向量 (3, - 4) (已知選項 (1)
是對的)是否垂直? 由於這兩個向量的內積為
3(a + s) - 4(b + t) 再次由式子
(96.3) 知道它們是垂直的. 這裡要注意雖然選項 (4), (5)
我們僅用式子 (96.3) 證明它們是對的, 這並不表示選項 (4), (5)
僅需 3x - 4y = 0 通過
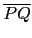 的中點就會成立.
事實上我們在處理過程中還是有用到 3x - 4y = 0 和
的中點就會成立.
事實上我們在處理過程中還是有用到 3x - 4y = 0 和
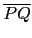 垂直這個事實, 即選項 (1). 所以這兩個選項還是需 3x - 4y = 0 是
垂直這個事實, 即選項 (1). 所以這兩個選項還是需 3x - 4y = 0 是
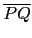 的中垂線這樣的假設才會成立.
的中垂線這樣的假設才會成立.
用代數的方法解決問題雖然有其便利性,
但是很多性質僅是利用一些等式推得無法理解其背後真正的原因.
例如本題選項 (4), (5) 感覺起來蠻特殊的性質,
用代數的方法便無法知道是什們因素造成這樣的結果. 我們就針對選項 (4),
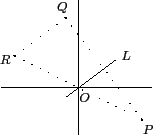
(5) 用幾何的方法處理, 以便了解其個中原委. 令點 (- s, - t) 為 R 點,
我們大致上可作下圖.
要注意原點 O 為
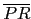 的中點, 且
的中點, 且
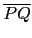 的中垂線 L 通過 O (因 L 的方程式為
3x - 4y = 0). 考慮三角形 PQR, 由於直線 L 通過
的中垂線 L 通過 O (因 L 的方程式為
3x - 4y = 0). 考慮三角形 PQR, 由於直線 L 通過
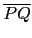 和
和
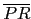 的中點, 故知 L 會與 QR 的連線平行. 證得選項 (4)
是對的. 至於選項 (5), 我們利用向量
的中點, 故知 L 會與 QR 的連線平行. 證得選項 (4)
是對的. 至於選項 (5), 我們利用向量
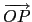 = -
= - 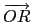 知
但已知 RQ 連線與 L 平行, 而 L 是
知
但已知 RQ 連線與 L 平行, 而 L 是
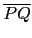 的中垂線, 故知
的中垂線, 故知
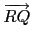 和
和
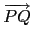 垂直. 證得選項 (5)
是對的. 從這個證明中我們發現 (4), (5) 這兩個選項會對的原因僅需
垂直. 證得選項 (5)
是對的. 從這個證明中我們發現 (4), (5) 這兩個選項會對的原因僅需
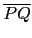 的中垂線 L 通過原點. 所以只要
的中垂線 L 通過原點. 所以只要
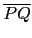 的中垂線方程式是如 cx + dy = 0 這樣的形式, 選項 (4), (5) 都會對.
這個結果前面用代數方法時很難被發現.
的中垂線方程式是如 cx + dy = 0 這樣的形式, 選項 (4), (5) 都會對.
這個結果前面用代數方法時很難被發現.


下一頁: 8
上一頁: 二、多選題
前一頁: 6
Li
2007-08-02
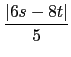
![]() 與向量 (3, - 4) 平行 (2) 線段
與向量 (3, - 4) 平行 (2) 線段
![]() 的長度等於
的長度等於
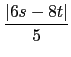
![]() +
+ ![]() 與向量
與向量
![]() 的內積必為 0.
的內積必為 0.
![]() 的中垂線上.
的中垂線上.
![]() = (a - s, b - t). 由此我們馬上得到下面兩個關係式:
= (a - s, b - t). 由此我們馬上得到下面兩個關係式:
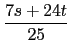 , b =
, b = 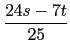 .
.