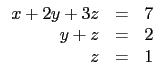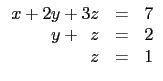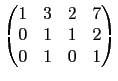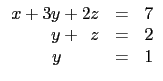(1)
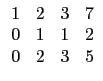
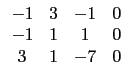
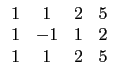
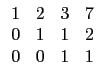
(1) ![]()
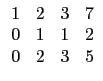
![]() (2)
(2) ![]()
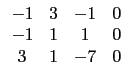
![]() (3)
(3) ![]()
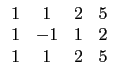
![]()
(4) ![]()
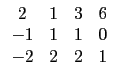
![]() (5)
(5) ![]()
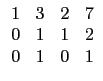
![]()
說明:高中課程中有關矩陣列運算的部份是在解多元一次聯立方程式時提及.
本題從矩陣是 3×4 矩陣, 以及選項來看,
應該傾向於與解聯立方程式連結, 而不是單純考列運算這個動作.
不過高中課程中對矩陣列運算與解聯立方程式間關係著墨不多. 看到此題,
或許有很多同學會``霧薩薩''不知道在考什麼.
讓我們先從純粹列運算的角度看這個問題. 一個矩陣經過列運算變成另一個矩陣, 這中間的步驟並不唯一. 所以若你找到一系列的列運算將一個矩陣轉換成另一個矩陣, 例如選項 (1) 的矩陣第 2 列乘上 -2 加到第 3 列就可以得到給定的矩陣, 那就沒問題; 但如果你一時無法找到列運算, 並不表示它們之間不能用列運算轉換, 除非你找到理由知道不可能. 所以如果只是單純地試試看每一個選項中的矩陣是否可經一系列的列運算轉換成給定的矩陣, 不只耗時而且可能出錯. 我們需要一個有系統的方法處理這樣的問題. 這裡最重要的關鍵是列運算式可逆的, 也就是說若矩陣 A 可以經列運算轉換成 B, 則 B 也可以經列運算轉換成 A. 因此若矩陣 A 和 B 都以經列運算轉換成 C, 那麼 A 和 B 之間當然就可以以經列運算轉換. 所以若我們嘗試將每一個矩陣經列運算轉換成某一種特殊形式的矩陣, 這種形式的矩陣需有一個特質就是每個矩陣皆可以轉換成這種形式的矩陣而且若換成這種形式的矩陣它是唯一的. 哪一種形式的矩陣有這樣的特質呢? 首先我們看每一個矩陣的第一行, 若第一行中有一個位置上的數字不是 0, 那麼我們就可以經列運算 將此行其他位置的數字變成 0 而原本位置的數字變成 1. 例如選項 (1) 的矩陣的第一行已達此目的可以不動, 而選項 (2) 的矩陣可以如下變換.
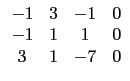
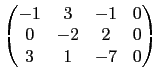
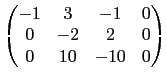
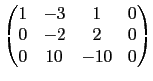 .
.
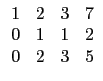
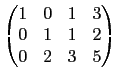
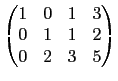 .
.
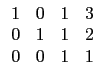

 .
.
若在第三行找不到不為 0 的數其左邊兩個位置皆為 0, 則此步就省略. 最後整理若有一列其前三行皆為 0, 則利用列運算將之置於最下後一列. 因為我們考慮的是 3×4 矩陣, 我們要處理的步驟就此完成. 總結我們得到的矩陣有以下特性, 即前三行中每一行至多有一位置為 1 其餘皆為 0. 除了前三行皆為 0 的情況, 我們不必處理, 其餘情況所得的矩陣共有以下這 7 種形式.

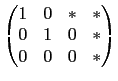
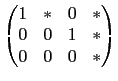
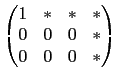
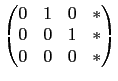
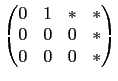
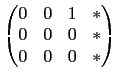 ,
,
由前面的步驟來看, 每一個矩陣都可以經列運算得到這裡列出矩陣的形式,
而且很容易看出不同形式的矩陣是無法用列運算互換的; 而相同形式的矩陣,
若是相異, 也無法用列運算互換.
因此我們只要將兩個矩陣經列運算轉換成以上形式, 若所得矩陣相同,
則兩矩陣間可以由列運算互換; 若所得矩陣相異,
則兩矩陣間不能由列運算互換. 例如題目所給定的矩陣和選項 (1), (5)
的矩陣皆可化成
 所以它們可以用列運算互換. 選項 (2)
的矩陣其第四行不管怎樣做列運算, 每個位置皆為 0
所以不會和上述矩陣相同, 而選項 (3), (4) 的矩陣前三行的 3×3
子矩陣, 經列運算會有一列全為 0, 和上述矩陣為不同形式的矩陣,
所以它們不可能經列運算得到題目給定的矩陣.
所以它們可以用列運算互換. 選項 (2)
的矩陣其第四行不管怎樣做列運算, 每個位置皆為 0
所以不會和上述矩陣相同, 而選項 (3), (4) 的矩陣前三行的 3×3
子矩陣, 經列運算會有一列全為 0, 和上述矩陣為不同形式的矩陣,
所以它們不可能經列運算得到題目給定的矩陣.
若對用 Gauss-Jordan 消去法解三元一次聯立方程組熟悉的話, 應該可以看出, 上面化成最後形式所做的列運算就是Gauss-Jordan 消去法的步驟. 其實本題若用解三元一次聯立方程組的角度處理, 可以很快解決, 不過處理之前我們還是先將原理講清楚. 我們可以用以下的方法將一般的 3×4 矩陣對應到一組三元一次聯立方程組.
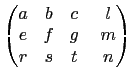
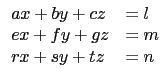
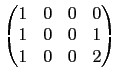 ,
, 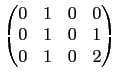
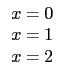 ,
, 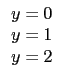
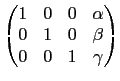 這一個矩陣, 所以利用前面所提列運算是可逆的,
知這兩個矩陣是可以用列運算互換的.
有無窮多解的情況也可用類似方法說明,
不過要依前面所提列運算最後其他的形式分別說明較為繁複我們就不多說了.
本題中給定的矩陣所對應的方程組為
這一個矩陣, 所以利用前面所提列運算是可逆的,
知這兩個矩陣是可以用列運算互換的.
有無窮多解的情況也可用類似方法說明,
不過要依前面所提列運算最後其他的形式分別說明較為繁複我們就不多說了.
本題中給定的矩陣所對應的方程組為