- (equiv1)
- 對所有 a
 S, 我們都有 a
S, 我們都有 a 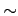 a (reflexivity).
a (reflexivity).
- (equiv2)
- 若 a
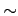 b, 則 b
b, 則 b 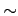 a (symmetry).
a (symmetry).
- (equiv3)
- 若 a
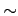 b 且 b
b 且 b 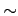 c, 則 a
c, 則 a 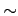 c
(transitivity).
c
(transitivity).
一般來說要將一個集合分類必須符合以下三個要素. 第一個就是, 自己和自己是同類的; 另一要素是若甲和乙是同類的則乙也必須和甲是同類的; 最後一個要素是如果甲和乙同類且乙和丙同類, 則甲必須和丙同類. 很多同學應該知道這樣的分類同類間的關係稱之為 equivalence relation. 我們還是用數學的方法給 equivalence relation 正式的定義.
有些同學可能會覺得奇怪既然 (equiv2) 說: 若 a ![]() b 則 b
b 則 b ![]() a.
那麼再利用 (equiv3) 我們可得 a
a.
那麼再利用 (equiv3) 我們可得 a ![]() a. 為什麼還要強調 (equiv1) 呢?
主要原因是 (equiv1) 強調是 S 中的任一元素 a 都須符合 a
a. 為什麼還要強調 (equiv1) 呢?
主要原因是 (equiv1) 強調是 S 中的任一元素 a 都須符合 a ![]() a.
如果我們只要求 (equiv2) 和 (equiv3), 那麼如果 S 中有一元素 a 在
S 中找不到任何的元素 b 使得 a
a.
如果我們只要求 (equiv2) 和 (equiv3), 那麼如果 S 中有一元素 a 在
S 中找不到任何的元素 b 使得 a ![]() b, 那麼 a 就不一定滿足
a
b, 那麼 a 就不一定滿足
a ![]() a 了. 因此會造成有的元素有可能沒有被分類到. 而符合
equivalence relation 的分類就確保每一個元素都會被分到某一類
(不過有可能某一類中只有一個元素).
a 了. 因此會造成有的元素有可能沒有被分類到. 而符合
equivalence relation 的分類就確保每一個元素都會被分到某一類
(不過有可能某一類中只有一個元素).
到底用 equivalence relation 分類有什麼好處呢? 首先當然是如前所說由
(equiv1) 可得每一個元素都會被分到某一類. 另外由 (equiv2) 和 (equiv3)
知兩個不同類的集合不會有交集; 這是因為如果 b 在 A 類且在 B
類中, 則在 A 類中的任一元素 a 因和 b 是同類的故 a ![]() b 而
B 類中的任一元素 c 因也和 b 同類故 b
b 而
B 類中的任一元素 c 因也和 b 同類故 b ![]() c. 故由 (equiv2) 和
(equiv3) 知 a
c. 故由 (equiv2) 和
(equiv3) 知 a ![]() c. 也就是說 A 中的所有元素和 B
中的所有元素都同類. 這和 A 與 B 是不同類的假設相矛盾.
總而言之利用一個 equivalent relation
我們可以將一集合分割成兩兩互不相交的類別.
c. 也就是說 A 中的所有元素和 B
中的所有元素都同類. 這和 A 與 B 是不同類的假設相矛盾.
總而言之利用一個 equivalent relation
我們可以將一集合分割成兩兩互不相交的類別.
接下來我們就來探討同餘的分類法.
要注意在談同餘時一定要先固定一個 m 才能說. 沒有 a 和 b 是同餘的說法, 你必須完整的說出 a 和 b 在除以什麼之下是同餘的才對.
雖然檢查 a, b 在除以 m 之下是否同餘, 依定義要檢查 a 和 b 除以 m 之餘數是否相同, 但事實上只要檢查 m 是否整除 a - b.
反之假設 a, b 除以 m 之餘數分別為 r1 及 r2, 即分別存在
h1, h2 ![]()
![]() 使得
a = mh1 + r1 及
b = mh2 + r2, 其中
0
使得
a = mh1 + r1 及
b = mh2 + r2, 其中
0![]() r1, r2 < m, 則知
a - b = m(h1 - h2) + (r1 - r2). 故由假設 m| a - b 得
m| r1 - r2. 又因
0
r1, r2 < m, 則知
a - b = m(h1 - h2) + (r1 - r2). 故由假設 m| a - b 得
m| r1 - r2. 又因
0![]() r1, r2 < m, 知
- m < r1 - r2 < m, 故由
m| r1 - r2 得 r1 = r2.
r1, r2 < m, 知
- m < r1 - r2 < m, 故由
m| r1 - r2 得 r1 = r2.
![]()
我們可以利用 Lemma 3.1.3 很快的得到 congruent relation 是一個 equivalent relation.
(2) 若
a ![]() b(mod m) 由 Lemma 3.1.3 知 m| a - b, 故由
m| b - a 得證
b
b(mod m) 由 Lemma 3.1.3 知 m| a - b, 故由
m| b - a 得證
b ![]() a(mod m).
a(mod m).
(3) 若
a ![]() b(mod m) 且
b
b(mod m) 且
b ![]() a(mod m), 則知 m| a - b 且
m| b - c. 故知
m|(a - b) + (b - c), 即 m| a - c. 也就是說
a
a(mod m), 則知 m| a - b 且
m| b - c. 故知
m|(a - b) + (b - c), 即 m| a - c. 也就是說
a ![]() c(mod m).
c(mod m).
![]()
由於同餘的概念用分類的看法是很好的分類且這樣的看法談論一些性質很方便, 今後我們經常會用 ``a 和 b 在 modulo m 之下是同類"的說法來表達: a 和 b 除以 m 之餘數相同.
既然用同餘的概念可將整數分類, 我們自然會問給定
m ![]()
![]() , 在 modulo
m 之下可以分成幾類呢? 所有整數在除以 m 之下的餘數總共可能為
0, 1,..., m - 1, 所以得知共有 m 類.
分類好後在每一類中我們可以挑一個代表元素來代表這一類,
且每類中僅挑出一個代表而不重複,
這樣所挑出的代表我們給它一個特別名稱.
, 在 modulo
m 之下可以分成幾類呢? 所有整數在除以 m 之下的餘數總共可能為
0, 1,..., m - 1, 所以得知共有 m 類.
分類好後在每一類中我們可以挑一個代表元素來代表這一類,
且每類中僅挑出一個代表而不重複,
這樣所挑出的代表我們給它一個特別名稱.
若 S 是一個 complete residue system modulo m, 則因整數在 modulo
m 之下是一個 equivalent relation, 所以 S
中的元素都會被分到某一類, 而且又已知 S 中的元素兩兩不同類,
再加上已知
![]() 在 modulo m 之下共能被分成 m 類, 所以由 S
的元素個數為 m 知, 每一類中都可在 S 中找到唯一的元素代表此類.
換言之, S 中的元素足以代表
在 modulo m 之下共能被分成 m 類, 所以由 S
的元素個數為 m 知, 每一類中都可在 S 中找到唯一的元素代表此類.
換言之, S 中的元素足以代表
![]() 在 modulo m 之下之分類. 例如
{0, 1,..., m - 1} 就是一個常用的 complete residue system modulo
m. 不過有時我們會因問題的需要選擇別種 complete residue system
modulo m.
在 modulo m 之下之分類. 例如
{0, 1,..., m - 1} 就是一個常用的 complete residue system modulo
m. 不過有時我們會因問題的需要選擇別種 complete residue system
modulo m.
利用同餘分類除了是一個 equivalent relation 之外, 還有許多很好的性質. 例如在下一節我們會介紹可以在各類之間定義運算. 另外在 modulo m 之下, 我們發現其實同類的元素和 m 之最大公因數其實是相同的.
特別的若 a 和 m 是 互質的, 則在 modulo m 之下和 a
同類的元素都和 m 互質. 也就是說若 S 是一個 complete residue
system modulo m, 只要找出 S 中有哪些元素和 m 互質,
那麼這些元素所代表的分類裡每個元素都和 m 互質. 在 modulo m
之下到底有幾類的元素會和 m 互質呢? 我們就考慮
S = {0, 1,..., m - 1} 這個 complete residue system modulo m 吧!
S 中和 m 互質的元素個數依 Euler ![]() -function 的定義就是
-function 的定義就是
![]() (m) 個, 故知整數在 modulo m 之下共有
(m) 個, 故知整數在 modulo m 之下共有 ![]() (m) 類的元素和
m 是互質的. 有時在處理問題時我們需要將這
(m) 類的元素和
m 是互質的. 有時在處理問題時我們需要將這 ![]() (m)
類的代表元素列出, 所以我們也給它一個特別名稱.
(m)
類的代表元素列出, 所以我們也給它一個特別名稱.
當 m 是一質數 p 時, {1,..., p - 1} 就是最常用的 reduced residue system modulo p.