

下一頁: Abelian p-groups
上一頁: Finite Abelian Groups
前一頁: Cauchy and Sylow's Theorems
現在我們來探討一些在一般 groups 不一定對但在 abelian groups 會對的一些性質.
當 G 是 abelian 時, 任取 a, b  G, 因
a . b = b . a
我們可以得
G, 因
a . b = b . a
我們可以得
(a . b)2 = (a . b) . (a . b) = a . (b . a) . b = a . (a . b) . b = a2 . b2.
利用數學歸納法我們很容易知對所有的
n 
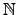 ,
,
(a . b)n = an . bn.
以下的 Lemma 告訴我們 G 是 abelian
的另一個好處:
Lemma 3.3.4
若
G 是一個 finite abelian group,
m 是一個大於 1 的整數且
m
整除
G 的 order. 考慮集合
M = {
g  G
G |
gm =
e}. 則
M 是
G
的一個 subgroup 且
M
{
e}.
証 明.
因
m > 1 故必存在一質數
p 使得
p |
m. 由 Theorem
3.3.2
知存在一元素
a  G
G 其 order 為
p. 故知
a e
e 且
ap =
e, 但
p |
m 故
am =
e. 也就是
a  M
M 故
M
{
e}.
現在證 M 是 G 的 subgroup. 首先證封閉性: 若 a, b  M, 即
am = e, bm = e. 故
(a . b)m = am . bm = e, 也就是說
a . b
M, 即
am = e, bm = e. 故
(a . b)m = am . bm = e, 也就是說
a . b  M. 接下來證反元素存在: 若 a
M. 接下來證反元素存在: 若 a  M, 因 am = e 故
(am)-1 . am = (am)-1 = (a-1)m. 然而又
(am)-1 . am = e, 故
(a-1)m = e. 也就是說
a-1
M, 因 am = e 故
(am)-1 . am = (am)-1 = (a-1)m. 然而又
(am)-1 . am = e, 故
(a-1)m = e. 也就是說
a-1  M.
M.

別忘了因 G 是 abelian 所以 M 會是 G 的一個 normal subgroup,
利用這一點我們可以得到以下有關 finite abelian group 非常重要的性質.
Lemma 3.3.5
設
G 是一個 finite abelian group, 且 |
G| =
pnm, 其中
p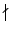 m
m.
令
P = {
g  G
G |
gpn =
e} and
M = {
g  G
G |
gm =
e},
則
G 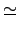 P
P×
M.
証 明.
由 Lemma
3.3.4 知
P 和
M 都是
G 的 normal subgroups.
要證明
G  P
P×
M, 我們得利用 Theorem
3.2.4 證明
G =
P . M 及
P  M
M = {
e} 就好. 這兩個性質都要用到
pn 和
m 互質來得到.
因為 pn 和 m 互質, 故存在整數 r 和 s 使得 rpn + sm = 1.
因此對任意的 a  G, 我們都可寫成
G, 我們都可寫成
a = arpn + sm = asm . arpn.
因為
((asm)pn = (apnm)s,
而 |
G| =
pnm, 由
Corollary
2.3.4 知
(asm)pn = e;
也就是說
asm  P
P. 同理知
arpn  M
M. 由此知任意的
G 中元素都可寫成一個
P
中的元素乘以
M 中的元素, 所以
G =
P . M.
另一方面, 若
g  P
P  M, 因 g
M, 因 g  M, 故 gm = e. 則由 Lemma
2.3.2 知
ord(g) | m. 同理得
ord(g) | pn. 也就是說
ord(g) 整除 gn 和 m 的最大公因數. 但 gn 和 m 互質, 故得
ord(g) = 1; 也就是說 g = e. 因此得證
P
M, 故 gm = e. 則由 Lemma
2.3.2 知
ord(g) | m. 同理得
ord(g) | pn. 也就是說
ord(g) 整除 gn 和 m 的最大公因數. 但 gn 和 m 互質, 故得
ord(g) = 1; 也就是說 g = e. 因此得證
P  M = {e}.
M = {e}.

Lemma 3.3.5 中 P 元素的個數是多少呢? 雖然是收集所有 G
中元素 g 符合 gpn = e 的元素但不表示其 order 就是 pn.
不過很巧妙的利用 Cauchy 的定理我們確實可以得到 | P| = pn.
Lemma 3.3.6
設
G 是一個 finite abelian group, 且 |
G| =
pnm,
其中
p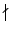 m
m. 令
P = {
g  G
G |
gpn =
e},
則
P 是
G
的一個 Sylow
p-subgroup, 而且
P 是
G 中唯一的 Sylow
p-subgroup.
証 明.
首先我們說明若令
M = {
g  G
G |
gm =
e}, 則
p
不能整除
M 的 order. 這是因為若
p 整除
M 的 order, 則由
Cauchy's Theorem 知
M 中存在一元素
a 其 order 為
p, 但
am =
e, 由 Lemma
2.3.2 知
p |
m. 這和假設
p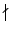 m
m 矛盾.
故
p 不能整除 |
M|.
接下來我們證 P 是一個 p-group. 假設除了 p 以外存在另一質數 q
整除 | P|, 則用和前面相同的方法可得 q | pn, 這又和 p, q
是相異質數矛盾. 換句話說 | P| 除了 p 以外不會有其他的質因數,
所以知存在
r 
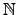 使得 | P| = pr.
使得 | P| = pr.
由 Lemma 3.3.5 知
G  P×M, 故
| G| = | P| . | M|. 因此得
P×M, 故
| G| = | P| . | M|. 因此得
| M| = | G|/| P| = pn - rm.
但
p 不整除
M, 故得
n =
r. 也就是說
P 是
G 的一個 Sylow
p-subgroup.
最後假設 P' 是 G 中任意的一個 Sylow p-subgroup. 因 | P'| = pn,
由 Lagrange 定理(Corollary 2.3.4) 知對於所有 a  P',
apn = e. 也就是說 a
P',
apn = e. 也就是說 a  P. 得證
P'
P. 得證
P'  P. 然而
| P'| = | P| = pn, 故 P' = P. 這證明了唯一性.
P. 然而
| P'| = | P| = pn, 故 P' = P. 這證明了唯一性.

這一次我們要強調 Lemma 3.3.6 是 abelian groups 特有的性質.
它告訴我們此時 Sylow p-subgroup 是長什麼樣子的, 而且是唯一的.
在一般的 group 這不一定是對的.
綜合以上幾個 Lemmas, 我們有以下的結論:
Proposition 3.3.7
設
G 是一個 finite abelian group, 其 order 為
| G| = p1n1 ... prnr,
其中
p1,...,
pr
是相異的質數. 令
Pi 是
G 中對每一個
pi 所對應的 Sylow
pi-subgroup,
i 
{1,...,
r}. 則
G 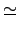 P1
P1×
... ×
Pr.
証 明.
若令
m =
p2n2 ... prnr, 且令
M = {
g  G
G |
gm =
e},
則由 Lemmas
3.3.5,
3.3.6 知
G  P1
P1×
M.
然而因
|
M| =
p2n2 ... prnr 故由數學歸納法可知
M  P2
P2×
... ×
Pn. 因此由 Lemma
3.2.5 得
G 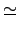 P1
P1×
M 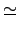 P1
P1×
P2×
... ×
Pr.



下一頁: Abelian p-groups
上一頁: Finite Abelian Groups
前一頁: Cauchy and Sylow's Theorems
Administrator
2005-06-18
![]() G, 因
a . b = b . a
我們可以得
G, 因
a . b = b . a
我們可以得
![]() M, 即
am = e, bm = e. 故
(a . b)m = am . bm = e, 也就是說
a . b
M, 即
am = e, bm = e. 故
(a . b)m = am . bm = e, 也就是說
a . b ![]() M. 接下來證反元素存在: 若 a
M. 接下來證反元素存在: 若 a ![]() M, 因 am = e 故
(am)-1 . am = (am)-1 = (a-1)m. 然而又
(am)-1 . am = e, 故
(a-1)m = e. 也就是說
a-1
M, 因 am = e 故
(am)-1 . am = (am)-1 = (a-1)m. 然而又
(am)-1 . am = e, 故
(a-1)m = e. 也就是說
a-1 ![]() M.
M.
![]()
![]() G, 我們都可寫成
G, 我們都可寫成
![]() P
P ![]() M, 因 g
M, 因 g ![]() M, 故 gm = e. 則由 Lemma
2.3.2 知
ord(g) | m. 同理得
ord(g) | pn. 也就是說
ord(g) 整除 gn 和 m 的最大公因數. 但 gn 和 m 互質, 故得
ord(g) = 1; 也就是說 g = e. 因此得證
P
M, 故 gm = e. 則由 Lemma
2.3.2 知
ord(g) | m. 同理得
ord(g) | pn. 也就是說
ord(g) 整除 gn 和 m 的最大公因數. 但 gn 和 m 互質, 故得
ord(g) = 1; 也就是說 g = e. 因此得證
P ![]() M = {e}.
M = {e}.
![]()
![]()
![]() 使得 | P| = pr.
使得 | P| = pr.
![]() P×M, 故
| G| = | P| . | M|. 因此得
P×M, 故
| G| = | P| . | M|. 因此得
![]() P',
apn = e. 也就是說 a
P',
apn = e. 也就是說 a ![]() P. 得證
P'
P. 得證
P' ![]() P. 然而
| P'| = | P| = pn, 故 P' = P. 這證明了唯一性.
P. 然而
| P'| = | P| = pn, 故 P' = P. 這證明了唯一性.
![]()