- 若 G 是 cyclic 則
G =
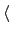 a
a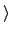 .
.
- 若 G 不是 cyclic 則在 G 中存在
b
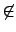
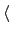 a
a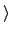 , 使得
ord(b) = p.
, 使得
ord(b) = p.
大家都知道 cyclic group 一定是 abelian. 不過若只知ㄧ個 group 是 abelian 它並不一定會是 cyclic. 下一個 Lemma 告訴我們一個判斷 abelian group 是否為 cyclic 的方法.
(1) 若 G 是 cyclic, 即 G 中存在一元素 x 使得
G = ![]() x
x![]() . 也就是說
ord(x) = pn. 然而已知 a 是 G 中元素 order
最大的之ㄧ. 所以知
ord(a) = pn (注意這個元素並不唯一,
所以我們並不可得 x = a). 換句話說 G 和
. 也就是說
ord(x) = pn. 然而已知 a 是 G 中元素 order
最大的之ㄧ. 所以知
ord(a) = pn (注意這個元素並不唯一,
所以我們並不可得 x = a). 換句話說 G 和
![]() a
a![]() 的元素個數一樣多, 即
G =
的元素個數一樣多, 即
G = ![]() a
a![]() .
.
(2) 若 G 不是 cyclic, 則當然
![]() a
a![]()
![]() G. 記
A =
G. 記
A = ![]() a
a![]() . 可知 quotient group G/A 仍是一個 abelian
p-group, 即
| G/A| = pn - r. 利用 Cauchy 定理 (Theorem
3.3.2) 知存在
. 可知 quotient group G/A 仍是一個 abelian
p-group, 即
| G/A| = pn - r. 利用 Cauchy 定理 (Theorem
3.3.2) 知存在
![]()
![]() G/A 使得
ord(
G/A 使得
ord(![]() ) = p. 也就是說
) = p. 也就是說
![]()
![]()
![]() 不過
不過
![]() =
= ![]() , 因此
x
, 因此
x ![]() A 但
xp
A 但
xp ![]() A. 因為
A =
A. 因為
A = ![]() a
a![]() , xp
, xp ![]() A 表示存在一整數 i
使得 xp = ai. 我們用反證法證明 p | i.
A 表示存在一整數 i
使得 xp = ai. 我們用反證法證明 p | i.
如果 p![]() i, 則由 Proposition 2.3.3 知
i, 則由 Proposition 2.3.3 知
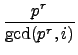 = pr.
= pr.
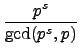 = ps - 1.
= ps - 1.
假設 i = pt, 令
b = a-t . x. 注意若 b ![]() A, 則因
x = at . b, 會導致 x
A, 則因
x = at . b, 會導致 x ![]() A, 這和
x
A, 這和
x ![]() A 相矛盾, 故知
b
A 相矛盾, 故知
b ![]() A,
且當然 b
A,
且當然 b![]() e (因 e
e (因 e ![]() A). 然而因 G 是 abelian,
bp = a-pt . xp. 利用 pt = i 及
ai = xp, 我們推得
bp = e. 由此可得
ord(b) = p. 這是因為由 Lemma 2.3.2 知
ord(b) | p. 但 p 是質數, 所以得
ord(b) = 1 or
ord(b) = p.
然而已知 b
A). 然而因 G 是 abelian,
bp = a-pt . xp. 利用 pt = i 及
ai = xp, 我們推得
bp = e. 由此可得
ord(b) = p. 這是因為由 Lemma 2.3.2 知
ord(b) | p. 但 p 是質數, 所以得
ord(b) = 1 or
ord(b) = p.
然而已知 b![]() e 即
ord(b)
e 即
ord(b)![]() 1, 故可得
ord(b) = p.
1, 故可得
ord(b) = p.
![]()
下一個 Lemma 告訴我們如果一個 abelian p-group 不是 cyclic 那麼它在某種程度上和 cyclic group 還是相差不遠.
接下來我們想用 B 來幫我們以數學歸納法證明這個 Lemma. 若 G 的 order 為 p, 由 Corollary 2.2.3 知 G 是一個 cyclic group. 若 | G| = pn. 假設此 Lemma 在所有 order 小於 pn 的 abelian p-groups 都對.
當然若 G 是 cyclic 則證明完成, 但 G 是有可能不是 cyclic 的. 若
G 不是 cyclic, 考慮 G/B 這一個 abelian group. 因
| G/B| = pn - 1, 故 G/B 是一個 order 小於 pn 的 abelian
p-group. 此時我們就可以用 induction 的假設,
不過要用這個假設我們得先在 G/B 中找到一個 order 最大的元素. 事實上
![]() 會是 G/B 中 order 最大的元素. 主要原因是由 Lemma
3.3.1 知對所有的
會是 G/B 中 order 最大的元素. 主要原因是由 Lemma
3.3.1 知對所有的
![]()
![]() G/B, 都有
ord(
G/B, 都有
ord(![]() )
)![]() ord(x). 又因
B
ord(x). 又因
B ![]()
![]() a
a![]() = {e} 故再由 Lemma
3.3.1 得
ord(
= {e} 故再由 Lemma
3.3.1 得
ord(![]() ) = ord(a). 因為 a 是 G 中 order
最大的元素, 故得在 G/B 中對任意的
) = ord(a). 因為 a 是 G 中 order
最大的元素, 故得在 G/B 中對任意的
![]()
![]() G/B 皆有
G/B 皆有
現在我們可以套用歸納的假設了. 由假設知有可能 G/B 是 cyclic,
要不然在 G/B 中存在一個 subgroup Q' 使得
G/B ![]()
![]()
![]()
![]() ×Q'.
×Q'.
若 G/B 是 cyclic, 由 Lemma 3.3.8 知
G/B = ![]()
![]()
![]() . 此時我們要證明
G
. 此時我們要證明
G ![]()
![]() a
a![]() ×B.
由 Theorem 3.2.4 知這相當於要證明
G = A . B 且
A
×B.
由 Theorem 3.2.4 知這相當於要證明
G = A . B 且
A ![]() B = {e} (別忘了 A, B 都是 normal). 不過由於我們已證得
A
B = {e} (別忘了 A, B 都是 normal). 不過由於我們已證得
A ![]() B = {e}, 所以只要證
G = A . B. 對任意的 x
B = {e}, 所以只要證
G = A . B. 對任意的 x ![]() G, 考慮
G, 考慮
![]()
![]() G/B. 則由於
G/B =
G/B. 則由於
G/B = ![]()
![]()
![]() , 故存在一整數
i 使得
, 故存在一整數
i 使得
![]() =
= ![]() . 這表示 x 和 ai 在 B
的分類下是同類的. 也就是
(ai)-1 . x
. 這表示 x 和 ai 在 B
的分類下是同類的. 也就是
(ai)-1 . x ![]() B.
換句話說存在一整數 j 使得
x = ai . bj. 得證 G
中的元素都可寫成一個 A 中元素乘上一個 B 中元素的形式, 即
G = A . B. 故加上
A
B.
換句話說存在一整數 j 使得
x = ai . bj. 得證 G
中的元素都可寫成一個 A 中元素乘上一個 B 中元素的形式, 即
G = A . B. 故加上
A ![]() B = {e} 得
G
B = {e} 得
G ![]() A×B.
A×B.
若 G/B 不是 cyclic 則由 induction 的假設知在 G/B 中存在一個
subgroup Q' 使得
G/B ![]()
![]()
![]()
![]() ×Q'. 利用
Theorem 3.2.4 知此時
G/B =
×Q'. 利用
Theorem 3.2.4 知此時
G/B = ![]()
![]()
![]() . Q' 且
. Q' 且
![]()
![]()
![]()
![]() Q' = {
Q' = {![]() }. 因為我們要把問題拉回到
G 來看, 利用 Correspondence 定理 (Corollary 2.7.3) 知在 G
中存在一個 subgroup Q 符合
B
}. 因為我們要把問題拉回到
G 來看, 利用 Correspondence 定理 (Corollary 2.7.3) 知在 G
中存在一個 subgroup Q 符合
B ![]() Q 且 Q/B = Q'. 我們要證明
G
Q 且 Q/B = Q'. 我們要證明
G ![]()
![]() a
a![]() ×Q.
×Q.
首先證
G = A . Q. 任取 x ![]() G, 由於
G, 由於
![]()
![]() G/B, 且
G/B =
G/B, 且
G/B = ![]()
![]()
![]() . Q/B, 故存在一整數 i 和 q
. Q/B, 故存在一整數 i 和 q ![]() Q
使得
Q
使得
最後要證
A ![]() Q = {e}. 若
x
Q = {e}. 若
x ![]() A
A ![]() Q, 由
x
Q, 由
x ![]() A =
A = ![]() a
a![]() 知 存在一整數 i 使得 x = ai. 故在 G/B 中
知 存在一整數 i 使得 x = ai. 故在 G/B 中
![]() =
= ![]() =
= ![]() . 另一方面 a
. 另一方面 a ![]() Q 故在 G/B 中
Q 故在 G/B 中
![]()
![]() Q/B = Q'. 也就是說
Q/B = Q'. 也就是說
Lemma 3.3.9 告訴我們什麼呢? 如果 G 是 abelian p-group, 且
| G| = pn. 則有可能 G 是 cyclic group: 若是如此則由 Theorem
3.1.1 知
G ![]()
![]() /pn
/pn![]() . G 也有可能不是 cyclic, 那麼
Lemma 3.3.9 就告訴我們若 G 中 order 最大的元素其 order 是
pn1, 則存在一個 subgroup Q 使得
G
. G 也有可能不是 cyclic, 那麼
Lemma 3.3.9 就告訴我們若 G 中 order 最大的元素其 order 是
pn1, 則存在一個 subgroup Q 使得
G ![]() (
(![]() /pn1
/pn1![]() )×Q. 這裡因 G 是 abelian p-group, 其
subgroup Q 當然也是 abelian p-group. 如果 Q 是 cyclic,
那麼我們就可得
G
)×Q. 這裡因 G 是 abelian p-group, 其
subgroup Q 當然也是 abelian p-group. 如果 Q 是 cyclic,
那麼我們就可得
G ![]() (
(![]() /pn1
/pn1![]() )×Q
)×Q ![]() (
(![]() /pn1
/pn1![]() )×(
)×(![]() /pn2
/pn2![]() ); 如果 Q 不是 cyclic
則再用一次 Lemma 3.3.9 知 Q 會 isomorphic to 一個 cyclic group
和 Q 的 subgroup 的 direct product. 這樣一直下去, 由於 G 的
order 是有限的經過有限次後一定會停. 我們可以有以下的結果:
); 如果 Q 不是 cyclic
則再用一次 Lemma 3.3.9 知 Q 會 isomorphic to 一個 cyclic group
和 Q 的 subgroup 的 direct product. 這樣一直下去, 由於 G 的
order 是有限的經過有限次後一定會停. 我們可以有以下的結果: