証 明.
我們利用前面介紹的 group action, 這裡我們令
m =
p,
H 是
Sp 中由
(1 2
... p) 這一個
p-cycle 所產生的 cyclic subgroup.
而
S = {(
a1,...,
ap)
 Gp
Gp |
a1 . a2 ... ap =
e}.
若
|
G| =
n 利用前面式子 (
4.2) 知
|
S| =
np - 1, 故由假設
p |
n 得
p 整除 |
S|. 也就是說
| S| 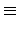 0(mod p) 0(mod p) |
(4.5) |
由 lemma
3.4.7 知
(1 2
... p) 這一個
p-cycle 的
order 為
p, 故知 |
H| =
p. 也就是說
H 是一個
p-group. 因此利用
Proposition
4.1.4 和式子 (
4.5) 知
|
S0|
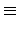
|
S|
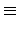
0(mod
p).
也就是說
p 整除 |
S0|.
不過由式子 (
4.4) 知
|
S0|

1, 再加上
p 整除 |
S0|,
也就是 |
S0| 是
p 的倍數且不是 0. 因此我們知
| S| > 1.
換句話說
S0 中除了已知的
(
e,
e,...,
e)
這個元素外還有其他的元素. 由式子 (
4.3), 我們知道在這些元素都是
(
a,
a,...,
a) 這種形式, 且
ap =
e. 因此得
a e
e 且
ap =
e,
也就是說
ord(
a) =
p.

回顧一下從前我們先證明了在 abelian group 情形下的 Cauchy 定理,
再利用它證得 abelian group 的 Sylow 定理. 將來我們也會用這一般 group
的 Cauchy 定理證明一般 group 的 Sylow 定理.