我們要推廣處理兩個整數的平方和的方法來處理四個整數的平方和問題. 首先我們有一個和式子 (7.1) 相對應的式子.
| (a2 + b2 + c2 + d2)(e2 + f2 + g2 + h2) | = | (ae + bf + cg + dh)2 + (af - be + ch - dg)2 | |
| + (ag - bh - ce + df )2 + (ah + bg - cf - de)2. |
利用式子 (7.2) 我們馬上有以下之結果.
由於每個大於 1 的整數都可以寫成質因數的乘積, 所以由 Lemma 7.3.8 我們很自然的要探討哪些質數可以寫成四個整數的平方和. 由於 2 和除以 4 餘 1 的質數皆可寫成兩個整數的平方和, 所以它們皆可寫成四個整數的平方和 (多餘的兩個補 0), 因此我們僅剩下要討論除以 4 餘 3 的質數. 我們可以推廣 Lemma 7.3.2 的方法 得到一個判別一個質數是否可以寫成四個整數的平方和的方法.
利用反證法, 假設 m![]() 1. 故由
1. 故由
![]()
![]() S 且
S 且 ![]() < p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m
< p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m ![]() S,
故存在
t, u, v, w
S,
故存在
t, u, v, w ![]()
![]() 使得
t2 + u2 + v2 + w2 = mp, 我們分成 m
是偶數及 m 是奇數兩種情況討論.
使得
t2 + u2 + v2 + w2 = mp, 我們分成 m
是偶數及 m 是奇數兩種情況討論.
(I) m 是偶數: 此時由於 t2 + u2 + v2 + w2 = mp 是偶數, 我們知 t, u, v, w 必皆為奇數; 皆為偶數偶; 或是其中兩個是奇數兩個是偶數. 在所有的情況之下我們都可以將 t, u, v, w 分成同奇同偶的兩對. 不失一般性, 我們假設 t, u 同奇同偶且 v, w 同奇同偶, 即 t + u, t - u, v + w 和 v - w 皆為偶數. 此時 (t + u)/2, (t - u)/2, (v + w)/2 和 (v - w)/2 皆為整數且
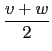 )2 + (
)2 + (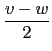 )2 =
)2 = (II) m 是奇數: 因為當 m 是奇數時
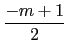 ,
,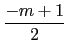 + 1,..., 0, 1,...,
+ 1,..., 0, 1,...,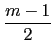 - 1,
- 1,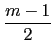 }
}
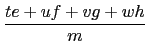 , U =
, U = 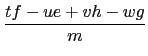 ,
,
 and W =
and W = 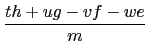 ,
,
我們證得若 m![]() 1 會造成 m 不是偶數且不是奇數的矛盾.
故由反證法知原假設 m
1 會造成 m 不是偶數且不是奇數的矛盾.
故由反證法知原假設 m![]() 1 不成立, 也就是說 m = 1. 故得證 p
可以寫成四個整數的平方和.
1 不成立, 也就是說 m = 1. 故得證 p
可以寫成四個整數的平方和.
![]()
接下來我們將利用 Lemma 7.3.9
來證明所有的正整數皆可寫成四個整數的平方和. 我們僅剩下要說明除以 4
餘 3 的質數可以寫成四個整數的平方和. 由於此時
x2 ![]() - 1(mod p) 無解, 我們要利用此特性找出一個
- 1(mod p) 無解, 我們要利用此特性找出一個
![]()
![]()
![]() 使得
x2
使得
x2 ![]() -
- ![]() (mod p) 有解. 由於此時
(mod p) 有解. 由於此時
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]() = -
= - ![]()
![]()
![]() , 得
, 得
![]()
![]()
![]() = 1 若且唯若
= 1 若且唯若
![]()
![]()
![]() = - 1. 所以我們必須找到
= - 1. 所以我們必須找到
![]()
![]()
![]() 使得
x2
使得
x2 ![]()
![]() (mod p) 無解. 這是可以辦到的,
因為
S = {1, 2,..., p - 1} 是 modulo p 的 reduced residue system,
若 p
(mod p) 無解. 這是可以辦到的,
因為
S = {1, 2,..., p - 1} 是 modulo p 的 reduced residue system,
若 p![]() a, 則
x2
a, 則
x2 ![]() a(mod p) 的解必和 S 中的某個元素在
modulo p 之下同餘. 也就是說
x2
a(mod p) 的解必和 S 中的某個元素在
modulo p 之下同餘. 也就是說
x2 ![]() a(mod p) 有解若且唯若存在
c
a(mod p) 有解若且唯若存在
c ![]() S 使得
c2
S 使得
c2 ![]() a(mod p). 所以我們只要將 S
中的每一個元素平方, 若 a 和平方後的某個數在 modulo p 之下同餘則
x2
a(mod p). 所以我們只要將 S
中的每一個元素平方, 若 a 和平方後的某個數在 modulo p 之下同餘則
x2 ![]() a(mod p) 有解; 反之, 若 a 和平方後每個數在 modulo p
之下皆不同餘則
x2
a(mod p) 有解; 反之, 若 a 和平方後每個數在 modulo p
之下皆不同餘則
x2 ![]() a(mod p) 無解. 然而若 c
a(mod p) 無解. 然而若 c ![]() S 則
p - c
S 則
p - c ![]() S 且
(p - c)2
S 且
(p - c)2 ![]() (- c)2
(- c)2 ![]() c(mod p), 又因為 p
是奇質數, 所以
c
c(mod p), 又因為 p
是奇質數, 所以
c ![]() p - c(mod p). 也就是說 S
中的元素平方後在 modulo p 之下僅有 (p - 1)/2 個不同餘類.
因此我們知道 S 中共有 (p - 1)/2 個元素 a 會使得
x2
p - c(mod p). 也就是說 S
中的元素平方後在 modulo p 之下僅有 (p - 1)/2 個不同餘類.
因此我們知道 S 中共有 (p - 1)/2 個元素 a 會使得
x2 ![]() a(mod p) 有解, 且有 (p - 1)/2 個元素 a 會使得
x2
a(mod p) 有解, 且有 (p - 1)/2 個元素 a 會使得
x2 ![]() a(mod p) 無解.
a(mod p) 無解.
現考慮
S = {1, 2,..., p - 1} 這一個 modulo p 的 reduced residue
system. 令
![]()
![]() S 是 S 中最小的數使得
x2
S 是 S 中最小的數使得
x2 ![]()
![]() (mod p) 無解, 也就是說
(mod p) 無解, 也就是說
![]()
![]()
![]() = - 1. 由於
= - 1. 由於
![]()
![]()
![]() = 1, 我們知
= 1, 我們知 ![]() > 1, 因此
> 1, 因此
![]() - 1
- 1 ![]() S, 且
x2
S, 且
x2 ![]()
![]() - 1(mod p) 有解 (因
- 1(mod p) 有解 (因 ![]() 是 S 中最小的數使得
x2
是 S 中最小的數使得
x2 ![]()
![]() (mod p) 無解). 另一方面
p
(mod p) 無解). 另一方面
p ![]() 3(mod 4), 所以
3(mod 4), 所以
![]()
![]()
![]() = - 1, 故得
= - 1, 故得
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]() = 1, 也就是說
x2
= 1, 也就是說
x2 ![]() -
- ![]() (mod p) 有解. 現令 a
(mod p) 有解. 現令 a ![]() S 是
x2
S 是
x2 ![]()
![]() - 1 之ㄧ解,
我們可選 a 使得
1
- 1 之ㄧ解,
我們可選 a 使得
1![]() a
a![]() (p - 1)/2. 這是因為若
(p + 1)/2
(p - 1)/2. 這是因為若
(p + 1)/2![]() a
a![]() p - 1, 則考慮 p - a, 此時
(p - a)2
p - 1, 則考慮 p - a, 此時
(p - a)2 ![]() (- a)2
(- a)2 ![]()
![]() - 1(mod p) 仍為
x2
- 1(mod p) 仍為
x2 ![]()
![]() - 1(mod p) 之ㄧ解且
1
- 1(mod p) 之ㄧ解且
1![]() p - a < (p - 1)/2. 同理我們也可找到 b
p - a < (p - 1)/2. 同理我們也可找到 b ![]() S 是
x2
S 是
x2 ![]() -
- ![]() (mod p) 之ㄧ解且
1
(mod p) 之ㄧ解且
1![]() b
b![]() (p - 1)/2. 現由於
(p - 1)/2. 現由於
現任取
n ![]()
![]() . 若 n = 1, 則 n 當然寫成四個整數的平方和. 若
n > 1, 則可將 n 寫成質因數之乘積
n = p1n1 ... prnr. 若
pi = 2 或
pi
. 若 n = 1, 則 n 當然寫成四個整數的平方和. 若
n > 1, 則可將 n 寫成質因數之乘積
n = p1n1 ... prnr. 若
pi = 2 或
pi ![]() 1(mod 4) 則 pi 可以寫成兩個整數的平方和,
故可以寫成四個整數的平方和. 若
pi
1(mod 4) 則 pi 可以寫成兩個整數的平方和,
故可以寫成四個整數的平方和. 若
pi ![]() 3(mod 4), 則由前知 pi
也可以寫成四個整數的平方和. 故利用 Lemma 7.3.8 知
n = p1n1 ... prnr 可以寫成四個整數的平方和.
3(mod 4), 則由前知 pi
也可以寫成四個整數的平方和. 故利用 Lemma 7.3.8 知
n = p1n1 ... prnr 可以寫成四個整數的平方和.
![]()
我們已介紹了一些基礎數論應有的基本知識, 本講義就此結束.