

下一頁: Sum of Four Squares
上一頁: 平方和問題
前一頁: 平方和問題
當一個正整數不是某個整數的平方時,
我們有興趣知道它是否可寫成兩個整數的平方和. 若 n
本身是某個整數的平方, 即存在
m 
 使得 n = m2, 當然我們可以將
n 寫成 n = m2 + 02.
所以我們可以將可寫成兩個整數的平方和的數視為平方數的推廣.
使得 n = m2, 當然我們可以將
n 寫成 n = m2 + 02.
所以我們可以將可寫成兩個整數的平方和的數視為平方數的推廣.
首先我們來看一個有趣的等式:
| (a2 + b2)(c2 + d2) = (ac + bd )2 + (ad - bc)2. |
(7.1) |
這個等式可以直接將等號兩邊展開來求證,
也可以用大家熟悉的複數運算來說明. 假設
z1 = a + bi, z2 = d + ci 
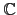 (這裡
(這裡
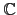 表示複數所成之集合, 而
i
表示複數所成之集合, 而
i 
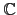 滿足
i2 = - 1).
我們知 z1, z1 的共軛複數分別為
滿足
i2 = - 1).
我們知 z1, z1 的共軛複數分別為
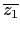 = a - bi,
= a - bi,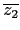 = d - ci
且
= d - ci
且
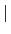 z1
z1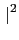 = z1
= z1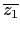 = a2 + b2 及
= a2 + b2 及
 z2
z2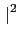 = z2
= z2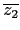 = c2 + d2. 因此
= c2 + d2. 因此
(
a2 +
b2)(
c2 +
d2) =
z1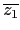 z2
z2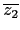
=
z1z2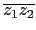
=
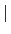
(
ad -
bc) + (
ac +
bd )
i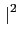
= (
ac +
bd )
2 + (
ad -
bc)
2.
利用式子 (7.1) 我們馬上有以下之結果.
証 明.
若
m =
a2 +
b2 且
n =
c2 +
d2, 其中
a,
b,
c,
d 

, 則利用式子
(
7.1) 知
mn = (
ac +
bd )
2 + (
ad -
bc)
2. 因
ac +
bd,
ad -
bc 

故知
mn 亦可以寫成兩個整數的平方和.

注意 Lemma 7.3.1 僅告訴我們當 m, n
皆可以寫成兩個整數的平方和時, mn 也可以寫成兩個整數的平方和;
它並沒有告訴我們若 m, n 中有一個不能寫成兩個整數的平方和時, mn
是否可以寫成兩個整數的平方和.
由於每個大於 1 的整數都可以寫成質因數的乘積, 所以由 Lemma
7.3.1
我們很自然的要探討哪些質數可以寫成兩個整數的平方和哪些質數不能. 由於
2 = 12 + 12, 即 2 可以寫成兩個整數的平方和,
因此以下我們僅考慮奇質數的情形. 利用 Lemma 7.3.1
我們可以得到一個判別一個質數是否可以寫成兩個整數的平方和的方法.
Lemma 7.3.2
假設
p 是一個質數. 若存在
a,
b 

使得
a2 +
b2 =
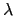 p
p,
其中
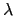


滿足
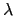
<
p, 則
p
可以寫成兩個整數的平方和.
証 明.
考慮集合
S = {
s 

| 存在
u,
v 

使得
u2 +
v2 =
sp}.
依照
S 的定義, 要證明
p 可以寫成兩個整數的平方和就等同於要證明
1
 S
S. 要如何知 1
 S
S 呢? 依假設知
S 為非空集合 (因
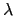
 S
S) 且
S 的元素皆為正整數, 所以 1
 S
S 若且唯若
S
中最小的元素就是 1 (注意依正整數的 well-ordering principle, 由於
S 不是空集合所以
S 中必存在最小的元素). 令
m  S
S 是
S
中最小的元素, 我們要證明
m = 1.
利用反證法, 假設 m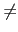 1. 故由
1. 故由
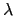
 S 且
S 且 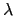 < p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m
< p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m  S,
故存在
u, v
S,
故存在
u, v 
 使得
u2 + v2 = mp, 我們分成 m 是偶數及 m
是奇數兩種情況討論.
使得
u2 + v2 = mp, 我們分成 m 是偶數及 m
是奇數兩種情況討論.
(I) m 是偶數: 此時由於
u2 + v2 = mp 是偶數, 我們知 u, v
必同奇同偶 (否則 u2 + v2 不會是偶數), 即 u + v 和 u - v 皆為偶數.
此時 (u + v)/2 和 (u - v)/2 皆為整數且
故知
m/2
 S
S 且
m/2 <
m, 此與
m 是
S 中最小的元素相矛盾.
(II) m 是奇數: 因為當 m 是奇數時
{
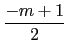
,
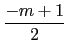
+ 1,..., 0, 1,...,
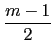
- 1,
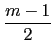
}
是一個
complete residue system modulo
m. 我們可找到
c,
d 

滿足
c  u
u(mod
m) 且
d  v
v(mod
m), 其中
- (
m - 1)/2
 c
c,
d
(
m - 1)/2. 注意這裡
c 和
d 不能同時等於 0, 這是因為如果
c =
d = 0
表示
u  v
v 
0(mod
m), 即
m|
u 且
m|
v. 因此
m2|
u2 +
v2 =
mp, 即
m|
p. 如此會和 1 <
m <
p 相矛盾, 故知
c 和
d
不同時為 0. 因為
c2 +
d2  u2
u2 +
v2(mod
m) 以及
u2 +
v2 =
mp, 我們得
c2 +
d2 
0(mod
m). 亦即存在
k 

使得
c2 +
d2 =
km. 注意因
c 和
d 不同時為 0, 故
k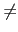
0.
另一方面因為
- (
m - 1)/2
 c
c,
d
(
m - 1)/2, 所以
c2 +
d2
(
m - 1)
2/4 + (
m - 1)
2/4 = (
m - 1)
2/2 <
m2, 故得 0 <
k <
m. 也就是說
k 

且
k <
m. 現在我們有兩個等式:
u2 +
v2 =
mp 以及
c2 +
d2 =
km.
利用式子 (
7.1) 得
(uc + vd )2 + (ud - vc)2 = m2kp.
又因為
u  c
c(mod
m) 且
v  d
d(mod
m), 我們得
uc +
vd  u2
u2 +
v2 
0(mod
m) and
ud -
vc  uv
uv -
uv 
0(mod
m).
也就是說
(
uc +
vd )/
m 

且
(
ud -
vc)/
m 

. 因此知
(
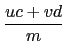
)
2 + (
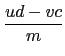
)
2 =
kp,
也就是說
kp
可以寫成兩個整數的平方和, 故又由
k 

知
k  S
S. 然而我們又知
k <
m, 此與
m 是
S 中最小的元素相矛盾.
我們證得若 m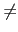 1 會造成 m 不是偶數且不是奇數這樣的矛盾.
故由反證法知原假設 m
1 會造成 m 不是偶數且不是奇數這樣的矛盾.
故由反證法知原假設 m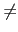 1 不成立, 也就是說 m = 1. 因此得證 p
可以寫成兩個整數的平方和.
1 不成立, 也就是說 m = 1. 因此得證 p
可以寫成兩個整數的平方和.

Lemma 7.3.2 的證明方法其實是類似於 descent
的方法都是由一個解得到更小的解而推得矛盾.
或許大家會疑惑為何同樣的推論方法, 一個會得到無解; 另一個卻推得有解.
這是因為在 descent 的方法推論中是沒有任何條件的,
所以若有正整數解則會沒有限制的推得無窮多個更小的正整數解而造成矛盾,
因此會得到無解的結論. 而這裡所用的方法中會得到比 m
更小的正整數是有條件的, 也就是說必須在 m > 1 的情形才可以.
因此同樣推得矛盾, 但此時矛盾會讓我們推得 m = 1, 所以有解.
希望這兩者邏輯上的差異, 大家都能了解. 另外 Lemma
7.3.2 證得存在的方法表面上好像只是邏輯推演,
並沒有告訴我們如何找到解.
事實上其解法過程中包含了找到解的方法. 我們來看一個具體的例子.
Example 7.3.3
考慮
p = 89. 由於
89

1(mod 4), 我們知存在
a 

使得
a2 
- 1(mod 89). 事實上當
a = 34 時,
a2 = 1156

- 1(mod 89), 我們有
(34)
2 + 1 = 13×89. 因為 13 < 89 故由 Lemma
7.3.2 知 89 可以寫成兩個整數的平方和. 我們要利用 Lemma
7.3.2 的證明方法將 89 寫成兩個整數的平方和.
對應到 Lemma 7.3.2 的證明, 我們知 13  S. 因 13
S. 因 13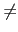 1,
我們要利用 13, 在 S 中找到更小的元素. 我們要找到 c, d 滿足
34
1,
我們要利用 13, 在 S 中找到更小的元素. 我們要找到 c, d 滿足
34  c(mod 13),
1
c(mod 13),
1  d(mod 13) 以及
-6
d(mod 13) 以及
-6 c, d
c, d 6.
很容易得知 c = - 5 且 d = 1. 接著我們考慮
c2 + d2 = 25 + 1 = 26 = 2×13. 故由式子 (7.1) 得
6.
很容易得知 c = - 5 且 d = 1. 接著我們考慮
c2 + d2 = 25 + 1 = 26 = 2×13. 故由式子 (7.1) 得
(34×(- 5) + 1)2 + (34 - (- 5))2 = 1692 + 392 = 2×132×89.
由於
169 = 13×13 且
39 = 3×13, 我們得
13
2 + 3
2 = 2×89, 也就是說 2
 S
S. 注意到我們已將 13
 S
S 降到 2
 S
S.
再利用處理偶數情況的方法, 將 2 縮小. 即得
(
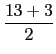
)
2 + (
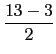
)
2 = 8
2 + 5
2 = 89.
在 Example 7.3.3 中我們利用
89  1(mod 4) 所以可以找到
a
1(mod 4) 所以可以找到
a 
 滿足
a2
滿足
a2  - 1(mod 89). 再適當的選取 a (即選取 a
夠小) 使得
a1 + 1 =
- 1(mod 89). 再適當的選取 a (即選取 a
夠小) 使得
a1 + 1 = 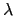 p, 其中
0 <
p, 其中
0 < 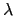 < p, 以便套用 Lemma
7.3.2. 在一般的情形, 當 p 是一質數滿足
p
< p, 以便套用 Lemma
7.3.2. 在一般的情形, 當 p 是一質數滿足
p  1(mod 4) 時, 我們都可以如此作. 所以我們有以下之結果.
1(mod 4) 時, 我們都可以如此作. 所以我們有以下之結果.
証 明.
由於
p 
1(mod 4), Theorem
5.4.1 告訴我們
x2 
- 1(mod
p) 有解. 亦即存在
a 

使得
a2 
- 1(mod
p).
由於
{1, 2,...,
p - 1} 是一個 reduced residue system modulo
p,
所以我們可以選取
1
 a
a p
p - 1 使得
a2 
- 1(mod
p)
(事實上可選取 1 <
a <
p/2). 因此存在
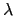


使得
a2 + 1 =
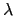 p
p. 又因為
a p
p - 1, 我們有
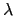 p
p =
a2 + 1

(
p - 1)
2 + 1 =
p2 - 2(
p - 1) <
p2. 也就是說
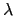
<
p, 故利用 Lemma
7.3.2 得證
p 可以寫成兩個整數的平方和.

接下來我們看怎樣的質數不能寫成兩個整數的平方和. 當
p  1(mod 4) 時, 在 Proposition 7.3.4 我們是利用此時
x2
1(mod 4) 時, 在 Proposition 7.3.4 我們是利用此時
x2  - 1(mod p) 有解證得 p 可以寫成兩個整數的平方和. 我們也可以利用當
p
- 1(mod p) 有解證得 p 可以寫成兩個整數的平方和. 我們也可以利用當
p  3(mod 4) 時,
x2
3(mod 4) 時,
x2  - 1(mod p) 無解證得 p
不可以寫成兩個整數的平方和.
- 1(mod p) 無解證得 p
不可以寫成兩個整數的平方和.
Lemma 7.3.5
假設
p 是一個質數滿足
p 
3(mod 4) 且
n 

滿足
p|
n.
若
a,
b 

使得
a2 +
b2 =
n, 則
p|
a 且
p|
b.
証 明.
我們要用反證法證明此定理. 不失一般性, 我們假設
p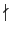 a
a. 此時由
a2 +
b2 =
n 且
p|
n 知
p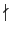 b
b, 否則由
a2 =
n -
b2 得
p|
a2
會造成與
p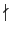 a
a 的假設相矛盾. 既然
a2 +
b2 =
n 且
p|
n, 我們得
a2 
-
b2(mod
p). 注意由於
a,
b 皆與
p 互質, 我們可以用
Legendre symbol 處理問題. 利用 Legendre symbol 的性質 (Lemma
5.3.2) 知
然而由
p 
3(mod 4) 以及 Theorem
5.4.1 我們知
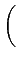
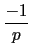
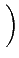
= - 1. 由此矛盾知
p|
a, 並由
b2 =
n -
a2 得
p|
b.

Lemma 7.3.5 證明的想法類似於 Proposition 7.1.1
所提的方法, 即利用探討 x2 + y2 = n 這個 Diophantine equation 在
modulo p 的情形來推得此 Diophantine equation 無解. 利用 Lemma
7.3.5 我們馬上得到以下之結果.
証 明.
我們用反證法. 假設存在
a,
b 

使得
a2 +
b2 =
p. 由於
p
是質數, 我們知
a,
b 皆不等於 0. 故知可取
a,
b 

滿足
1
 a
a p
p - 1 且
1
 b
b p
p - 1. 此時
a,
b 皆與
p 互質故與 Lemma
7.3.5 的結果相矛盾. 由此矛盾知
p 不能寫成兩個整數的平方和.

知道了哪些質數可以寫成兩個整數的平方和,
哪些質數不可以寫成兩個整數的平方和.
接下來我們就來探討哪些正整數可以寫成兩個整數的平方和. 給定一正整數
n. 若 n = 1 當然可寫成兩個整數的平方和. 若 n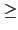 2, 首先我們將
n 作質因數的分解. 我們可以將 2 和除以 4 餘 1 的質因數忽略,
因為它們可以寫成兩個整數的平方和. 而若 n 有除以 4 餘 3 的質因數,
我們又可以將有平方的部份忽略, 因為它們也可以寫成兩個整數的平方和.
由此看出質因數分解後的次數是重要的, 我們特別用以下名詞的定義: 若
n = p1n1 ... prnr, 其中這些 pi 是相異質數. 我們稱
pi 是 n 的質因數且 ni 是 pi 的次數. 例如
2250 = 2×32×53, 我們稱 2250 有 2 次 3 的質因數且有 3 次 5
的質因數. 依此定義我們有以下之結果.
2, 首先我們將
n 作質因數的分解. 我們可以將 2 和除以 4 餘 1 的質因數忽略,
因為它們可以寫成兩個整數的平方和. 而若 n 有除以 4 餘 3 的質因數,
我們又可以將有平方的部份忽略, 因為它們也可以寫成兩個整數的平方和.
由此看出質因數分解後的次數是重要的, 我們特別用以下名詞的定義: 若
n = p1n1 ... prnr, 其中這些 pi 是相異質數. 我們稱
pi 是 n 的質因數且 ni 是 pi 的次數. 例如
2250 = 2×32×53, 我們稱 2250 有 2 次 3 的質因數且有 3 次 5
的質因數. 依此定義我們有以下之結果.
Theorem 7.3.7
假設
n 

. 則
n 可以寫成兩個整數的平方和若且唯若
n
沒有任何的除以 4 餘 3 的質因數其次數是奇數.
証 明.
假設
n 沒有任何的除以 4 餘 3 的質因數其次數是奇數.
我們僅需考慮
n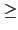
2 的情形. 此時可將
n 質因數分解成
n = 2n0q1n1 ... qrnr . p12m1 ... ps2ms,
其中
qi,
pj 皆為相異的奇質數且
qi 
1(mod 4) 及
pj 
3(mod 4). 由於我們可將
n 寫成
n = 2n0q1n1 ... qrnr . (p1m1 ... psms)2,
而 2 可以寫成兩個整數的平方和,
q1,...,
qr
可以寫成兩個整數的平方和 (Proposition
7.3.4) 以及
(
p1m1 ... psms)
2 可以寫成兩個整數的平方和
(因為是一個平方數), 故由 Lemma
7.3.1 知
n
可以寫成兩個整數的平方和.
反之, 若
p  3(mod 4) 是 n 的一個質因數且其次數為 2k + 1,
即
n = p2k + 1n', 其中 p
3(mod 4) 是 n 的一個質因數且其次數為 2k + 1,
即
n = p2k + 1n', 其中 p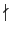 n'. 我們用反證法證明 n
不可以寫成兩個整數的平方和. 假設存在
a, b
n'. 我們用反證法證明 n
不可以寫成兩個整數的平方和. 假設存在
a, b 
 使得 a2 + b2 = n.
則由 Lemma 7.3.5 知 p| a 且 p| b. 令 a = prc 且 b = psd,
其中 c, d 皆與 p 互質且
r, s
使得 a2 + b2 = n.
則由 Lemma 7.3.5 知 p| a 且 p| b. 令 a = prc 且 b = psd,
其中 c, d 皆與 p 互質且
r, s 
 . 不失一般性我們假設 2r
. 不失一般性我們假設 2r 2s, 我們要證明 2k + 1 > 2r. 假設 2k + 1 < 2r, 由
p2rc2 + p2sd2 = p2k + 1n' 知
n' = p2r - 2k - 1c2 + p2s - 2k - 1d2. 又因為
2s - 2k - 1
2s, 我們要證明 2k + 1 > 2r. 假設 2k + 1 < 2r, 由
p2rc2 + p2sd2 = p2k + 1n' 知
n' = p2r - 2k - 1c2 + p2s - 2k - 1d2. 又因為
2s - 2k - 1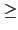 2r - 2k - 1 > 0 知
p| n'. 此與 p
2r - 2k - 1 > 0 知
p| n'. 此與 p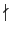 n' 相矛盾, 故知 2k + 1 > 2r. 再由
p2rc2 + p2sd2 = p2k + 1n' 知
n' 相矛盾, 故知 2k + 1 > 2r. 再由
p2rc2 + p2sd2 = p2k + 1n' 知
c2 + p2s - 2rd2 = c2 + (ps - rd )2 = p2k + 1 - 2rn',
即
p2k + 1 - 2rn' 可以寫成
c 和
ps - rd 的平方和.
由於
p 
3(mod 4),
p|
p2k + 1 - 2rn' 且
p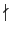 c
c, 此與
Lemma
7.3.5 的結果相矛盾, 故知
n 不可以寫成兩個整數的平方和.

例如
2250 = 2×32×53 中唯一的除以 4 餘 3 的質因數是 3,
且 3 的次數為 2 是偶數, 所以 2250 可以寫成兩個整數的平方和.
事實上
2250 = 452 + 152. 另外
6174 = 2×32×73 中除以 4
餘 3 的質因數是 3 和 7, 其中 7 的次數為 3 是奇數, 所以 6174
無法寫成兩個整數的平方和.


下一頁: Sum of Four Squares
上一頁: 平方和問題
前一頁: 平方和問題
Li
2007-07-12
![]() 1. 故由
1. 故由
![]()
![]() S 且
S 且 ![]() < p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m
< p 知 1 < m < p. 我們希望在 S 中找到比 m 更小的數而得到矛盾. 由於 m ![]() S,
故存在
u, v
S,
故存在
u, v ![]()
![]() 使得
u2 + v2 = mp, 我們分成 m 是偶數及 m
是奇數兩種情況討論.
使得
u2 + v2 = mp, 我們分成 m 是偶數及 m
是奇數兩種情況討論.
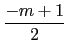 ,
,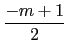 + 1,..., 0, 1,...,
+ 1,..., 0, 1,...,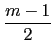 - 1,
- 1,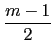 }
}
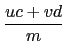 )2 + (
)2 + (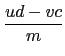 )2 = kp,
)2 = kp,
![]() 1 會造成 m 不是偶數且不是奇數這樣的矛盾.
故由反證法知原假設 m
1 會造成 m 不是偶數且不是奇數這樣的矛盾.
故由反證法知原假設 m![]() 1 不成立, 也就是說 m = 1. 因此得證 p
可以寫成兩個整數的平方和.
1 不成立, 也就是說 m = 1. 因此得證 p
可以寫成兩個整數的平方和.
![]()
![]() S. 因 13
S. 因 13![]() 1,
我們要利用 13, 在 S 中找到更小的元素. 我們要找到 c, d 滿足
34
1,
我們要利用 13, 在 S 中找到更小的元素. 我們要找到 c, d 滿足
34 ![]() c(mod 13),
1
c(mod 13),
1 ![]() d(mod 13) 以及
-6
d(mod 13) 以及
-6![]() c, d
c, d![]() 6.
很容易得知 c = - 5 且 d = 1. 接著我們考慮
c2 + d2 = 25 + 1 = 26 = 2×13. 故由式子 (7.1) 得
6.
很容易得知 c = - 5 且 d = 1. 接著我們考慮
c2 + d2 = 25 + 1 = 26 = 2×13. 故由式子 (7.1) 得
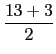 )2 + (
)2 + (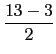 )2 = 82 + 52 = 89.
)2 = 82 + 52 = 89.
![]() 1(mod 4) 所以可以找到
a
1(mod 4) 所以可以找到
a ![]()
![]() 滿足
a2
滿足
a2 ![]() - 1(mod 89). 再適當的選取 a (即選取 a
夠小) 使得
a1 + 1 =
- 1(mod 89). 再適當的選取 a (即選取 a
夠小) 使得
a1 + 1 = ![]() p, 其中
0 <
p, 其中
0 < ![]() < p, 以便套用 Lemma
7.3.2. 在一般的情形, 當 p 是一質數滿足
p
< p, 以便套用 Lemma
7.3.2. 在一般的情形, 當 p 是一質數滿足
p ![]() 1(mod 4) 時, 我們都可以如此作. 所以我們有以下之結果.
1(mod 4) 時, 我們都可以如此作. 所以我們有以下之結果.
![]() 1(mod 4) 時, 在 Proposition 7.3.4 我們是利用此時
x2
1(mod 4) 時, 在 Proposition 7.3.4 我們是利用此時
x2 ![]() - 1(mod p) 有解證得 p 可以寫成兩個整數的平方和. 我們也可以利用當
p
- 1(mod p) 有解證得 p 可以寫成兩個整數的平方和. 我們也可以利用當
p ![]() 3(mod 4) 時,
x2
3(mod 4) 時,
x2 ![]() - 1(mod p) 無解證得 p
不可以寫成兩個整數的平方和.
- 1(mod p) 無解證得 p
不可以寫成兩個整數的平方和.
![]() 2, 首先我們將
n 作質因數的分解. 我們可以將 2 和除以 4 餘 1 的質因數忽略,
因為它們可以寫成兩個整數的平方和. 而若 n 有除以 4 餘 3 的質因數,
我們又可以將有平方的部份忽略, 因為它們也可以寫成兩個整數的平方和.
由此看出質因數分解後的次數是重要的, 我們特別用以下名詞的定義: 若
n = p1n1 ... prnr, 其中這些 pi 是相異質數. 我們稱
pi 是 n 的質因數且 ni 是 pi 的次數. 例如
2250 = 2×32×53, 我們稱 2250 有 2 次 3 的質因數且有 3 次 5
的質因數. 依此定義我們有以下之結果.
2, 首先我們將
n 作質因數的分解. 我們可以將 2 和除以 4 餘 1 的質因數忽略,
因為它們可以寫成兩個整數的平方和. 而若 n 有除以 4 餘 3 的質因數,
我們又可以將有平方的部份忽略, 因為它們也可以寫成兩個整數的平方和.
由此看出質因數分解後的次數是重要的, 我們特別用以下名詞的定義: 若
n = p1n1 ... prnr, 其中這些 pi 是相異質數. 我們稱
pi 是 n 的質因數且 ni 是 pi 的次數. 例如
2250 = 2×32×53, 我們稱 2250 有 2 次 3 的質因數且有 3 次 5
的質因數. 依此定義我們有以下之結果.
![]() 3(mod 4) 是 n 的一個質因數且其次數為 2k + 1,
即
n = p2k + 1n', 其中 p
3(mod 4) 是 n 的一個質因數且其次數為 2k + 1,
即
n = p2k + 1n', 其中 p![]() n'. 我們用反證法證明 n
不可以寫成兩個整數的平方和. 假設存在
a, b
n'. 我們用反證法證明 n
不可以寫成兩個整數的平方和. 假設存在
a, b ![]()
![]() 使得 a2 + b2 = n.
則由 Lemma 7.3.5 知 p| a 且 p| b. 令 a = prc 且 b = psd,
其中 c, d 皆與 p 互質且
r, s
使得 a2 + b2 = n.
則由 Lemma 7.3.5 知 p| a 且 p| b. 令 a = prc 且 b = psd,
其中 c, d 皆與 p 互質且
r, s ![]()
![]() . 不失一般性我們假設 2r
. 不失一般性我們假設 2r![]() 2s, 我們要證明 2k + 1 > 2r. 假設 2k + 1 < 2r, 由
p2rc2 + p2sd2 = p2k + 1n' 知
n' = p2r - 2k - 1c2 + p2s - 2k - 1d2. 又因為
2s - 2k - 1
2s, 我們要證明 2k + 1 > 2r. 假設 2k + 1 < 2r, 由
p2rc2 + p2sd2 = p2k + 1n' 知
n' = p2r - 2k - 1c2 + p2s - 2k - 1d2. 又因為
2s - 2k - 1![]() 2r - 2k - 1 > 0 知
p| n'. 此與 p
2r - 2k - 1 > 0 知
p| n'. 此與 p![]() n' 相矛盾, 故知 2k + 1 > 2r. 再由
p2rc2 + p2sd2 = p2k + 1n' 知
n' 相矛盾, 故知 2k + 1 > 2r. 再由
p2rc2 + p2sd2 = p2k + 1n' 知