

下一頁: Elementary Row Operations
上一頁: Systems of Linear Equations
前一頁: Systems of Linear Equations
解一次聯立方程組
所謂 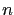 元一次的方程式就是有
元一次的方程式就是有 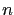 個未知數 (variable) 的一次方程式
(linear equation). 例如
個未知數 (variable) 的一次方程式
(linear equation). 例如
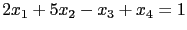 就是一個
就是一個 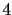 元一次的聯立方程組 (當然也可看成是
元一次的聯立方程組 (當然也可看成是 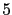 元或更高元).
元或更高元). 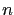 元一次的方程式抽象的表示法就是
元一次的方程式抽象的表示法就是
其中這些
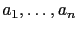 和
和 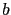 都是實數, 而這些
都是實數, 而這些 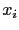 表未知數. 當我們有多個
表未知數. 當我們有多個 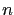 元一次的方程式要討論它們的共同解時,
就稱為解一次聯立方程組 (system of linear equations).
一般抽象的表示法
表示有
元一次的方程式要討論它們的共同解時,
就稱為解一次聯立方程組 (system of linear equations).
一般抽象的表示法
表示有 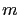 個
個 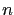 元一次方程式所成的方程組. 這裡
元一次方程式所成的方程組. 這裡
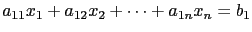 表示第一個方程式,
表示第一個方程式,
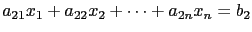 表示第二個方程式, 而當
表示第二個方程式, 而當
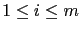 時, 第
時, 第 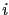 個方程式就是
個方程式就是
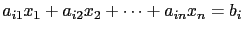 , 所以最後一個(即第
, 所以最後一個(即第
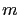 個)方程式就是
個)方程式就是
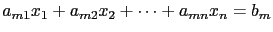 .
這裡
.
這裡
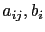 皆為實數, 這些實數才是真正影響到聯立方程組的因素,
所以我們也可特別把它們標明出來, 令
然後將上面的聯立方程式用
皆為實數, 這些實數才是真正影響到聯立方程組的因素,
所以我們也可特別把它們標明出來, 令
然後將上面的聯立方程式用
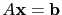 來表示.
通常我們會稱矩陣
來表示.
通常我們會稱矩陣 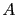 為此聯立方程式的係數矩陣.
一個矩陣的一個橫排稱為一個 row (列), 而一個豎排稱為一個 column (行).
我們算 row 時是從上而下來數的, 也就是說最上面的一個 row 稱為第一個
row, 下一個 row 稱為第二個 row, 依此類推. 而算 column
是由左而右來數的, 也就是說最左邊的一個 column 稱為第一個 column,
再往右一個 column 稱為第二個 column, 依此類推. 大家可以看出矩陣
為此聯立方程式的係數矩陣.
一個矩陣的一個橫排稱為一個 row (列), 而一個豎排稱為一個 column (行).
我們算 row 時是從上而下來數的, 也就是說最上面的一個 row 稱為第一個
row, 下一個 row 稱為第二個 row, 依此類推. 而算 column
是由左而右來數的, 也就是說最左邊的一個 column 稱為第一個 column,
再往右一個 column 稱為第二個 column, 依此類推. 大家可以看出矩陣 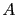 的 row 對應的就是此聯立方程組的方程式, 第一個 row
對應到第一個方程式, 第二個 row 對應到第二個方程式, 依此類推. 而
column 對應到的是方程組的未知數, 第一個 column 對應到的是未知數
的 row 對應的就是此聯立方程組的方程式, 第一個 row
對應到第一個方程式, 第二個 row 對應到第二個方程式, 依此類推. 而
column 對應到的是方程組的未知數, 第一個 column 對應到的是未知數
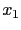 的係數, 第二個 column 對應到的是未知數
的係數, 第二個 column 對應到的是未知數 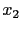 的係數, 依此類推.
注意這裡
的係數, 依此類推.
注意這裡
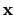 表示是一個未知的向量而且我們將向量
表示是一個未知的向量而且我們將向量
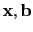 都寫成 column vector (行向量) 是為了配合將來矩陣乘法的寫法.
目前大家只要記住這也是聯立方程式的一種表示法即可.
都寫成 column vector (行向量) 是為了配合將來矩陣乘法的寫法.
目前大家只要記住這也是聯立方程式的一種表示法即可.
例如解聯立方程組
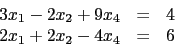 |
(2.1) |
我們就可以表成
注意這裡係數矩陣多出
![\begin{displaymath}\left[
\begin{array}{c}
0 \\
0 \\
\end{array}\right]\end{displaymath}](img370.gif) 這個 column 因為
這個 column 因為 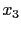 的係數為 0.
的係數為 0.
為何要探討解多元一次聯立方程組呢?
事實上解多元一次聯立方程式和線性代數的許多問題息息相關. 例如在
1.3 節中我們提到 span 的概念. 若
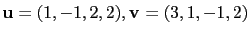 我們要問
我們要問
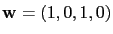 是否在
是否在
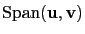 中就等同於問是否存在
中就等同於問是否存在
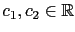 使得
使得
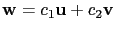 . 利用向量相等的定義, 這表示
. 利用向量相等的定義, 這表示
亦即要解
這一聯立方程組. 又如要問哪些向量
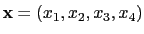 會同時滿足
會同時滿足
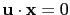 且
且
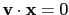 , 就等同於要解聯立方程組
將來我們還會碰到許多和解聯立方程組有關的問題,
這裡我們就不再多談而將重點放在如何解一個多元一次聯立方程組.
, 就等同於要解聯立方程組
將來我們還會碰到許多和解聯立方程組有關的問題,
這裡我們就不再多談而將重點放在如何解一個多元一次聯立方程組.
過去學習解一次聯立方程組的方法不外加減消去法或高斯消去法,
它們的原理都是一樣的, 即利用以下三種基本方法:
- 變換式子的順序
- 將某一式乘上一非零實數
- 將某一式乘上一實數後加到另一式上
利用這三種基本方法將方程式的某些變數消去, 最後求出解來.
當然這裡有些問題是要探討的:
第一就是要消到甚麼地步才可確認可求出解來?
第二就是為什麼經過這些過程所得的解救會是原方程組的解?
在本節中我們將先介紹一個較有系統的方法解聯立方程組的步驟,
讓大家知道何時就可確認此方程組有解或無解, 且有解時如何求解.
下一節我們再說明為何每一個聯立方程組都可以利用這個方式找到其解集合.
當我們要解
這一個聯立方成組時, 先寫出如下的 augmented matrix
(增廣矩陣)
例如式子 (2.1) 中的聯立方程組所對應的 augmented
matrix 為
換言之, 若我們要解
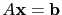 這一個聯立方成組,
就要寫下
這一個聯立方成組,
就要寫下
![$ [A\mid\mathbf{b}]$](img385.gif) 這一個 matrix. 反之一個 augmented matrix
這一個 matrix. 反之一個 augmented matrix
![$ [A\mid\mathbf{b}]$](img385.gif) 就對應到一個聯立方程組
就對應到一個聯立方程組
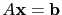 .
.
接下來我們將如加減消去法的三種步驟, 利用所謂的 elementary row
operation (基本列運算) 處理這個 augmented matrix. 所謂 elementary
row operation 即表示對矩陣進行如下三種的列運算:
- 將矩陣的某兩個 row 對調
- 將矩陣的某一個 row 乘上一非零實數
- 將矩陣的某一個 row 乘上一實數後加到另一個 row.
大家應很容易看出一個 augmented matrix 經過以上這三種列運算後所得的
augmented matrix
所對應的聯立方程組就是前面所提加減消去法的三種步驟所得的方程組.
我們的目的就是要將 augmented matrix
![$ [A\mid\mathbf{b}]$](img385.gif) 中的係數矩陣
中的係數矩陣 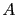 利用這三種 elementary row operation 化成所謂的 echelon form.
利用這三種 elementary row operation 化成所謂的 echelon form.
我們先解釋一下何謂 echelon form. 首先我們將矩陣每一個 row
從左到右來看第一個不為 0 的項稱為這個 row 的 leading entry,
因為每一個係數矩陣中的元素對應到聯立方程組中某個變數的係數, 所以
leading entry 若是變數 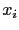 的係數, 我們就說這個 leading entry
發生在
的係數, 我們就說這個 leading entry
發生在 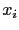 的位置. 要注意, 這也等同於這個 leading entry 是位於從左到右算來第
的位置. 要注意, 這也等同於這個 leading entry 是位於從左到右算來第 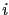 個 column. 例如矩陣
個 column. 例如矩陣
第一個 row 的 leading entry 為 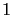 不過因為第一個 row
還有其他位置
不過因為第一個 row
還有其他位置 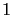 , 所以我們特別要說明第一個 row 的 leading entry
發生在
, 所以我們特別要說明第一個 row 的 leading entry
發生在 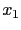 的位置, 而第二個 row 和第三個 row 的 leading entry
分別為
的位置, 而第二個 row 和第三個 row 的 leading entry
分別為 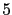 和
和 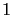 且發生的位置皆在
且發生的位置皆在 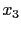 .
.
所謂一個矩陣是 echelon form 表示這個矩陣沒有 leading entry 的 row
(即該 row 每一項皆為 0) 必需在最下方, 而有 leading entry 的 row 其
leading entry 所在位置從上到下來看是往右移的. 換言之, 若上一個 row
的 leading entry 所在的位置是 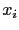 , 而下一個 row 的 lading entry 是
, 而下一個 row 的 lading entry 是
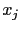 , 則必需
, 則必需 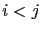 . 例如上一個矩陣並非 echelon form, 因為第 3 個
row 和第 2 個 row 的 leading entry 的位置皆為
. 例如上一個矩陣並非 echelon form, 因為第 3 個
row 和第 2 個 row 的 leading entry 的位置皆為 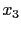 , 並未右移.
另外矩陣
, 並未右移.
另外矩陣
都不是 echelon form, 因為前一個矩陣全為 0 的 row
並未置於最下方, 而後一個矩陣第 3 個 row 的 leading entry 在第 2 個
row 的 leading entry 的左方. 至於矩陣
就是 echelon form. 當一個矩陣是 echelon form 時,
我們稱每一個 row 的 leading entry 為 pivot, 而 pivot
所在的位置我們稱為 pivot variable.
當我們將 augmented matrix
![$ [A\mid\mathbf{b}]$](img385.gif) 利用 elementary row
operation 將之化成
利用 elementary row
operation 將之化成
![$ [A'\mid\mathbf{b'}]$](img391.gif) 且
且 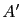 為 echelon form 後.
為 echelon form 後.
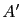 有兩種情形. 一種情形為
有兩種情形. 一種情形為 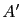 每一個 row 皆不全為 0; 另一種為
每一個 row 皆不全為 0; 另一種為
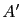 有些 row 全為 0. 我們分別依這兩種情形來討論聯立方程組的解.
有些 row 全為 0. 我們分別依這兩種情形來討論聯立方程組的解.
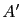 每一個 row 皆不全為 0: 此時聯立方程組一定有解.
我們又可細分成兩種情況.
每一個 row 皆不全為 0: 此時聯立方程組一定有解.
我們又可細分成兩種情況.
- 第一種情況是每一個變數
(variable)
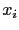 皆為 pivot variable. 亦即 pivot
的個數等於方程組``元''(未知數)的個數 (即係數矩陣
皆為 pivot variable. 亦即 pivot
的個數等於方程組``元''(未知數)的個數 (即係數矩陣 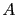 的
column 個數).
例如
此時 echelon form 的 pivot variable 分別為
的
column 個數).
例如
此時 echelon form 的 pivot variable 分別為
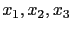 恰就是聯立方程組的未知數
恰就是聯立方程組的未知數
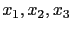 .
在這種情況之下此聯立方程組會有唯一解,
而且我們可利用從下往上``代回''的方式求得解. 例如前面的 augmented
matrix 所對應的聯立方程組為
所以我們從最下面的
.
在這種情況之下此聯立方程組會有唯一解,
而且我們可利用從下往上``代回''的方式求得解. 例如前面的 augmented
matrix 所對應的聯立方程組為
所以我們從最下面的
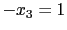 可得
可得 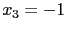 . 再將
. 再將 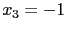 代入其上一式
代入其上一式
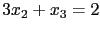 , 得
, 得
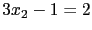 , 即
, 即 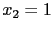 . 最後將
. 最後將
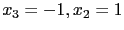 代入
代入
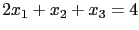 , 得
, 得 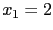 . 故得其解為
. 故得其解為
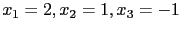 .
.
- 第二種情況是有些
variable
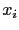 不是 pivot variable. 也就是方程組元的個數多於 pivot
的個數. 例如
此時 echelon form 的 pivot variable 分別為
不是 pivot variable. 也就是方程組元的個數多於 pivot
的個數. 例如
此時 echelon form 的 pivot variable 分別為
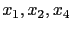 少於立方程組的未知數
少於立方程組的未知數
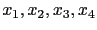 .
在此情形之下此聯立方程組會有無窮多解. 要得到這種方程組所有的解,
首先我們要找到 free variables. 所謂 free variable
指的是方程組除了 pivot variable 以外的 variable. 例如前面這個例子,
.
在此情形之下此聯立方程組會有無窮多解. 要得到這種方程組所有的解,
首先我們要找到 free variables. 所謂 free variable
指的是方程組除了 pivot variable 以外的 variable. 例如前面這個例子,
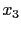 就是 free variable. Free variable 意指它可以任意取值, 所以找到
free variables 後你可以給它們任意的參數,
然後再利用如上一情況中由下往上代回的方式找到聯立方成組所有的解.
例如上一個 augmented matrix 所對應的聯立方程組為
首先令 free variable
就是 free variable. Free variable 意指它可以任意取值, 所以找到
free variables 後你可以給它們任意的參數,
然後再利用如上一情況中由下往上代回的方式找到聯立方成組所有的解.
例如上一個 augmented matrix 所對應的聯立方程組為
首先令 free variable 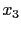 為一參數
為一參數 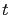 (表示它可以是任意實數
(表示它可以是任意實數
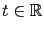 ). 接著我們從最下面的
). 接著我們從最下面的
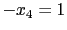 可得
可得 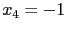 . 再將
. 再將
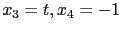 代入其上一式
代入其上一式
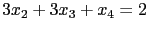 , 得
, 得
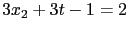 , 即
, 即 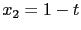 . 最後將
. 最後將
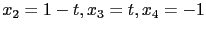 代入
代入
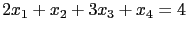 , 得
, 得 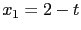 . 故得其解為
. 故得其解為
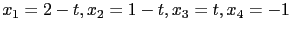 , 其中
, 其中 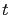 為任意實數. 因為
為任意實數. 因為 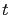 可以是任意實數, 由此我們也知此方程組有無窮多解.
可以是任意實數, 由此我們也知此方程組有無窮多解.
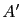 有些 row 全為
0: 此時聯立方程組可能無解, 我們分成兩種情況:
有些 row 全為
0: 此時聯立方程組可能無解, 我們分成兩種情況:
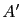 有一個 row 全為 0 但
有一個 row 全為 0 但
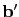 在該 row 不為 0.
例如
在該 row 不為 0.
例如
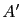 最後一個 row 皆為 0, 但
最後一個 row 皆為 0, 但
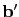 在該 row 的位置為
在該 row 的位置為
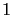 . 在此情形之下聯立方程組一定無解. 例如上一個 augmented matrix
其最後一個 row 所對應的方程式為
但不管
. 在此情形之下聯立方程組一定無解. 例如上一個 augmented matrix
其最後一個 row 所對應的方程式為
但不管
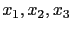 代任何的實數都無法滿足
代任何的實數都無法滿足
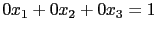 ,
所以此方程組無解.
,
所以此方程組無解.
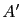 全為 0 的 row,
全為 0 的 row,
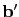 在該 row 亦為 0. 例如
這兩個 augmented matrices 皆為這種情形.
在此情形之下聯立方程組一定有解. 事實上在此情形我們可以忽略全為 0
的 row, 例如前兩個 augmented matrices 所對應的方程組和
所對應的方程組一樣. 所以我們可依前面 (1)
在該 row 亦為 0. 例如
這兩個 augmented matrices 皆為這種情形.
在此情形之下聯立方程組一定有解. 事實上在此情形我們可以忽略全為 0
的 row, 例如前兩個 augmented matrices 所對應的方程組和
所對應的方程組一樣. 所以我們可依前面 (1) 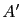 每一個 row
皆不全為 0 的情況找出聯立方程組所有的解.
每一個 row
皆不全為 0 的情況找出聯立方程組所有的解.
我們要強調, 絕不會有 pivot 的個數多於方程組 variables (元)
的個數的情形發生. 這是因為當係數矩陣 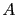 是 echelon form 時, 每一個
column 最多僅能有一個 pivot (因為不能有兩個 leading term
在同一個位置), 所以 pivot 的個數不能多於 column 的個數. 而
是 echelon form 時, 每一個
column 最多僅能有一個 pivot (因為不能有兩個 leading term
在同一個位置), 所以 pivot 的個數不能多於 column 的個數. 而 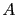 的
column 個數表示的就是此聯立方程組 variables 的個數, 因此 pivot
的個數不會多於 variables 的個數.
的
column 個數表示的就是此聯立方程組 variables 的個數, 因此 pivot
的個數不會多於 variables 的個數.
在這一節中我們介紹解一次聯立方程組
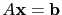 的步驟.
也就是先將 augmented matrix
的步驟.
也就是先將 augmented matrix
![$ [A\mid\mathbf{b}]$](img385.gif) 利用 elementary row
operations 化成
利用 elementary row
operations 化成
![$ [A'\mid\mathbf{b'}]$](img391.gif) 其中
其中 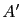 為 echelon form 的情形.
再利用上面談論的情況找出聯立方程組的解. 下一節中我們將說明為何可利用
elementary row operations 將
為 echelon form 的情形.
再利用上面談論的情況找出聯立方程組的解. 下一節中我們將說明為何可利用
elementary row operations 將 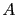 變成 echelon form
變成 echelon form 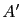 ,
且要說明為何這樣所得的解便是原方程組的解.
,
且要說明為何這樣所得的解便是原方程組的解.


下一頁: Elementary Row Operations
上一頁: Systems of Linear Equations
前一頁: Systems of Linear Equations
Cellist
2010-12-08
![]() 元一次的方程式就是有
元一次的方程式就是有 ![]() 個未知數 (variable) 的一次方程式
(linear equation). 例如
個未知數 (variable) 的一次方程式
(linear equation). 例如
![]() 就是一個
就是一個 ![]() 元一次的聯立方程組 (當然也可看成是
元一次的聯立方程組 (當然也可看成是 ![]() 元或更高元).
元或更高元). ![]() 元一次的方程式抽象的表示法就是
元一次的方程式抽象的表示法就是
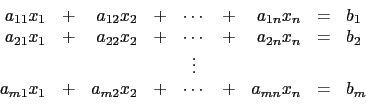
![\begin{displaymath}A=\left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1...
...
b_1 \\
b_2 \\
\vdots \\
b_m \\
\end{array}\right],\end{displaymath}](img361.gif)
![\begin{displaymath}\left[\begin{array}{rrrr}
3 & -2 & 0 & 9 \\
2 & 2 & 0 & -...
...ght]=\left[
\begin{array}{c}
4 \\
6 \\
\end{array}\right]\end{displaymath}](img369.gif)
![]() 我們要問
我們要問
![]() 是否在
是否在
![]() 中就等同於問是否存在
中就等同於問是否存在
![]() 使得
使得
![]() . 利用向量相等的定義, 這表示
. 利用向量相等的定義, 這表示
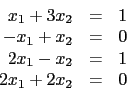
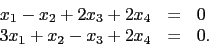
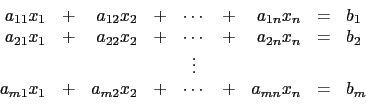
![\begin{displaymath}\left[
\begin{array}{cccc\vert c}
a_{11} & a_{12} & \cdots &...
...a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \\
\end{array}\right]\end{displaymath}](img383.gif)
![$\displaystyle \left[\begin{array}{rrrr\vert l}
3 & -2 & 0 & 9 &4\\
2 & 2 & 0 & -4 &6\\
\end{array}\right]$](img384.gif)
![]() 的係數, 我們就說這個 leading entry
發生在
的係數, 我們就說這個 leading entry
發生在 ![]() 的位置. 要注意, 這也等同於這個 leading entry 是位於從左到右算來第
的位置. 要注意, 這也等同於這個 leading entry 是位於從左到右算來第 ![]() 個 column. 例如矩陣
個 column. 例如矩陣
![\begin{displaymath}\left[
\begin{array}{ccccc}
1 & 2 & 1 & 1 & 4 \\
0 & 0 & 5 & 0 & 2 \\
0 & 0 & 1 & -1 & 1 \\
\end{array}\right]\end{displaymath}](img386.gif)
![]() , 而下一個 row 的 lading entry 是
, 而下一個 row 的 lading entry 是
![]() , 則必需
, 則必需 ![]() . 例如上一個矩陣並非 echelon form, 因為第 3 個
row 和第 2 個 row 的 leading entry 的位置皆為
. 例如上一個矩陣並非 echelon form, 因為第 3 個
row 和第 2 個 row 的 leading entry 的位置皆為 ![]() , 並未右移.
另外矩陣
, 並未右移.
另外矩陣
![\begin{displaymath}\left[
\begin{array}{cccc}
1 & 2 & -1 & 0 \\
0 & 0 & 0 & ...
...\
0 & 0 & 2 & -1 \\
3 & 0 & 0 & 0 \\
\end{array}\right]\end{displaymath}](img389.gif)
![\begin{displaymath}\left[
\begin{array}{ccccc}
0 & 2 & 1 & 1 & 4 \\
0 & 0 & ...
... 0 & 0 & -1 & 1 \\
0 & 0 & 0 & 0 & 0 \\
\end{array}\right]\end{displaymath}](img390.gif)
![]() 利用 elementary row
operation 將之化成
利用 elementary row
operation 將之化成
![]() 且
且 ![]() 為 echelon form 後.
為 echelon form 後.
![]() 有兩種情形. 一種情形為
有兩種情形. 一種情形為 ![]() 每一個 row 皆不全為 0; 另一種為
每一個 row 皆不全為 0; 另一種為
![]() 有些 row 全為 0. 我們分別依這兩種情形來討論聯立方程組的解.
有些 row 全為 0. 我們分別依這兩種情形來討論聯立方程組的解.
![\begin{displaymath}\left[
\begin{array}{ccc\vert c}
2 & 1 & 1 & 4 \\
0 & 3 & 1 & 2 \\
0 & 0 & -1 & 1 \\
\end{array}\right]\end{displaymath}](img393.gif)
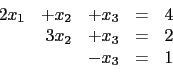
![\begin{displaymath}\left[
\begin{array}{cccc\vert c}
2 & 1 & 3&1 & 4 \\
0 & 3 & 3&1 & 2 \\
0 & 0 & 0&-1 & 1 \\
\end{array}\right]\end{displaymath}](img405.gif)
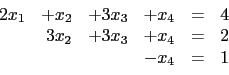
![\begin{displaymath}[A'\mid\mathbf{b'}]=\left[
\begin{array}{ccc\vert c}
2 & 1 &...
...\\
0 & 3 & 1 & 2 \\
0 & 0 & 0 & 1 \\
\end{array}\right]\end{displaymath}](img422.gif)
![\begin{displaymath}\left[
\begin{array}{cc\vert c}
2 & 1 & 4 \\
0 & 3 & 2 \\...
...
0 & 3 & 3&1 & 2 \\
0 & 0 & 0&0 & 0 \\
\end{array}\right]\end{displaymath}](img425.gif)
![\begin{displaymath}\left[
\begin{array}{cc\vert c}
2 & 1 & 4 \\
0 & 3 & 2 \\...
...
2 & 1 & 3&1 & 4 \\
0 & 3 & 3&1 & 2 \\
\end{array}\right]\end{displaymath}](img426.gif)
![]() 是 echelon form 時, 每一個
column 最多僅能有一個 pivot (因為不能有兩個 leading term
在同一個位置), 所以 pivot 的個數不能多於 column 的個數. 而
是 echelon form 時, 每一個
column 最多僅能有一個 pivot (因為不能有兩個 leading term
在同一個位置), 所以 pivot 的個數不能多於 column 的個數. 而 ![]() 的
column 個數表示的就是此聯立方程組 variables 的個數, 因此 pivot
的個數不會多於 variables 的個數.
的
column 個數表示的就是此聯立方程組 variables 的個數, 因此 pivot
的個數不會多於 variables 的個數.
![]() 的步驟.
也就是先將 augmented matrix
的步驟.
也就是先將 augmented matrix
![]() 利用 elementary row
operations 化成
利用 elementary row
operations 化成
![]() 其中
其中 ![]() 為 echelon form 的情形.
再利用上面談論的情況找出聯立方程組的解. 下一節中我們將說明為何可利用
elementary row operations 將
為 echelon form 的情形.
再利用上面談論的情況找出聯立方程組的解. 下一節中我們將說明為何可利用
elementary row operations 將 ![]() 變成 echelon form
變成 echelon form ![]() ,
且要說明為何這樣所得的解便是原方程組的解.
,
且要說明為何這樣所得的解便是原方程組的解.