如果我們得到 2.1 節 (2)(a) 的情形 (即 ![]() 有一個 row 全為 0
但
有一個 row 全為 0
但
![]() 在該 row 不為 0), 在該節已說明此時方程組無解.
所以我們只要探討有解的情形. 首先回顧一下在 2.1
所提求解的方法: 首先我們要找到 free variables,
也就是是方程組除了 pivot variable 以外的 variable. 接著給這些 free
variable 任意的參數值,
然後再利用由下往上代回的方式找到聯立方成組所有的解. 若無 free
variable, 就直接由下往上一步一步求值即可.
在該 row 不為 0), 在該節已說明此時方程組無解.
所以我們只要探討有解的情形. 首先回顧一下在 2.1
所提求解的方法: 首先我們要找到 free variables,
也就是是方程組除了 pivot variable 以外的 variable. 接著給這些 free
variable 任意的參數值,
然後再利用由下往上代回的方式找到聯立方成組所有的解. 若無 free
variable, 就直接由下往上一步一步求值即可.
由於可以忽略 augmented matrix 全為 0 的 row,
所以我們可假設係數矩陣 ![]() 沒有一個 row 全為 0. 因為
沒有一個 row 全為 0. 因為 ![]() 為
echelon form, 這也表示
為
echelon form, 這也表示 ![]() 每一個 row 皆有 leading entry 且為 pivot.
以下就是 pivot 對聯立方程組的解之重要性.
每一個 row 皆有 leading entry 且為 pivot.
以下就是 pivot 對聯立方程組的解之重要性.
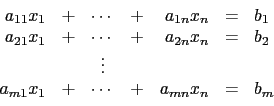
![\begin{displaymath}A=\left[
\begin{array}{ccc} a_{11} & \cdots & a_{1n} \\
a_...
...& \vdots \\
a_{m1} & \cdots & a_{mn} \\
\end{array}\right]\end{displaymath}](img452.gif)
相對於 pivot variable 我們知道對於 free variable 我們可以隨意取任何的實數而得到一組解, 所以我們有以下 free variable 對解的影響.
現若 ![]() 是 free variable, 這表示我們可以設定
是 free variable, 這表示我們可以設定 ![]() 為任意實數,
再一步一步往上代求得聯立方程組的一組解, 所以對任意的實數
為任意實數,
再一步一步往上代求得聯立方程組的一組解, 所以對任意的實數 ![]() , 方程組
, 方程組
![]() 皆可找到一組解其
皆可找到一組解其 ![]() 為
為 ![]() .
.
若 ![]() 為
為 ![]() 的一個 free variable, 其中
的一個 free variable, 其中
![]() 且已知
且已知
![]() 為方程組
為方程組
![]() 的一組解. 換言之,
的一組解. 換言之,
![]() 皆滿足方程組 pivot 的位置在
皆滿足方程組 pivot 的位置在 ![]() 右方所對應的那些方程式. 由於
右方所對應的那些方程式. 由於 ![]() 可取任意的實數且不會影響
可取任意的實數且不會影響
![]() 的取值, 所以我們可令
的取值, 所以我們可令 ![]() 且
且
![]() 一步一步代回求得聯立方程組的一組解.
一步一步代回求得聯立方程組的一組解.
![]()
Lemma 2.3.1 和 Lemma 2.3.2 有許多應用. 例如當 ![]() 是
echelon form 時若聯立方程組
是
echelon form 時若聯立方程組
![]() 已知有一個解
已知有一個解
![]() 且
且
![]() 每一個都是 pivot variable,
則由 Lemma 2.3.1 知聯立方程組
每一個都是 pivot variable,
則由 Lemma 2.3.1 知聯立方程組
![]() 的解僅能是
的解僅能是
![]() . 換句話說此方程組的解唯一. 另一方面, 若
若聯立方程組
. 換句話說此方程組的解唯一. 另一方面, 若
若聯立方程組
![]() 已知有解 且
已知有解 且
![]() 中有 free
variable, 則由 Lemma 2.3.2 知聯立方程組
中有 free
variable, 則由 Lemma 2.3.2 知聯立方程組
![]() 會有無窮多解.
會有無窮多解.
當我們給一個矩陣時, 有許多種方法將之化為 echelon form, 而且化成的 echelon form 很可能不一樣. 不過利用 Lemma 2.3.1 和 Lemma 2.3.2 我們可以得到這些 echelon form 雖然可能不一樣, 但他們 pivot 的所在位置都會一致.
我們要用反證法處理. 假設 ![]() 和
和 ![]() 有 pivot variable 不一致,
不失一般性我們就假設對
有 pivot variable 不一致,
不失一般性我們就假設對 ![]() 來說
來說 ![]() 是 pivot variable 但對
是 pivot variable 但對 ![]() 來說
來說 ![]() 不是 pivot variable (故為 free variable). 假設
不是 pivot variable (故為 free variable). 假設 ![]() ,
這表示方程組
,
這表示方程組
![]() 的解中
的解中 ![]() 的取值是唯一的 (Lemma
2.3.1), 事實上
的取值是唯一的 (Lemma
2.3.1), 事實上 ![]() 一定為 0; 但
一定為 0; 但
![]() 的解中
的解中
![]() 的取值卻可以是任意的實數 (Lemma 2.3.2).
這和此二方程組有相同的解相矛盾. 現若
的取值卻可以是任意的實數 (Lemma 2.3.2).
這和此二方程組有相同的解相矛盾. 現若
![]() . 利用
. 利用
![]() 已是這兩聯立方程組的解, 我們知道方程組
已是這兩聯立方程組的解, 我們知道方程組
![]() 的解中一定找不到一組解其
的解中一定找不到一組解其
![]() 的取值皆為 0 但
的取值皆為 0 但 ![]() 的取值不是 0 (Lemma 2.3.1); 另一方面
Lemma 2.3.2 告訴我們
的取值不是 0 (Lemma 2.3.1); 另一方面
Lemma 2.3.2 告訴我們
![]() 的解中一定可找到一組解其
的解中一定可找到一組解其
![]() 的取值皆為 0 但
的取值皆為 0 但 ![]() 的取值不是 0 (事實上
的取值不是 0 (事實上 ![]() 可以是任意實數). 這又和
可以是任意實數). 這又和
![]() 此二方程組有相同的解相矛盾.
故由反證法知
此二方程組有相同的解相矛盾.
故由反證法知
![]() 和
和 ![]() 的 pivot variables 是一致的.
的 pivot variables 是一致的.
![]()
現在我們回來說明當 ![]() 是 echelon form 時, 前幾節所述解聯立方程組
是 echelon form 時, 前幾節所述解聯立方程組
![]() 的方法所求得的解就是所有的解. 也就是說若
的方法所求得的解就是所有的解. 也就是說若
![]() 為
為
![]() 的一組解,
我們要說明這組解確實可由前面 2.1 節所提的方法得到.
為了方便起見我們令前面 2.1 節所提的方法所得的解所成的集合為
的一組解,
我們要說明這組解確實可由前面 2.1 節所提的方法得到.
為了方便起見我們令前面 2.1 節所提的方法所得的解所成的集合為 ![]() . 現若
. 現若 ![]() 為
pivot variable, 則由 Lemma 2.3.1 知,
為
pivot variable, 則由 Lemma 2.3.1 知, ![]() 的所有解中
的所有解中 ![]() 的取值一定也為
的取值一定也為 ![]() . 若
. 若 ![]() 為 free variable, 則因
為 free variable, 則因 ![]() 的解中
的解中
![]() 可為任意值, 故
可為任意值, 故 ![]() 中一定有一組解其
中一定有一組解其 ![]() 的取值為
的取值為 ![]() .
也就是說不管
.
也就是說不管 ![]() 是否為 pivot variable,
是否為 pivot variable, ![]() 中必有一組解其
中必有一組解其 ![]() 的取值為
的取值為 ![]() . 現若
. 現若 ![]() 為 pivot variable, 再由 Lemma
2.3.1 知這一組解
為 pivot variable, 再由 Lemma
2.3.1 知這一組解
![]() 的取值必為
的取值必為
![]() ; 而若
; 而若 ![]() 為 free variable, 則因
為 free variable, 則因 ![]() 的解中
的解中 ![]() 可為任意值且其取值不影響到
可為任意值且其取值不影響到 ![]() 的取值, 故知
的取值, 故知 ![]() 中必有一組解其
中必有一組解其
![]() 的取值為
的取值為
![]() .
如此一直下去我們知道
.
如此一直下去我們知道 ![]() 中必有一組解其
中必有一組解其
![]() 的取值為
的取值為
![]() .
.
我們已完全了解整個解聯立方程組的步驟與原理了.
在求解的過程中還可以進一步將 echelon form 化為所謂的 reduced echelon
form. Reduced echelon form 事實上仍為 echelon form,
不過再加上兩個限制, 第一個限制是每一個 pivot 需為 ![]() . 另一個限制為
pivot 的位置上方全為 0. 要注意, 依定義 echelon form 的 pivot
位置下方已全為 0 所以 reduced echelon form 每一個 pivot 所在的
column, 除了自己需為
. 另一個限制為
pivot 的位置上方全為 0. 要注意, 依定義 echelon form 的 pivot
位置下方已全為 0 所以 reduced echelon form 每一個 pivot 所在的
column, 除了自己需為 ![]() 外其他部分皆為 0. 例如
外其他部分皆為 0. 例如
![\begin{displaymath}A=\left[
\begin{array}{cccc}
1 & 2 & 0 & 0 \\
0 & 0 & 3 &...
...\
0 & 1 & 1 & 2 \\
0 & 0 & 1 & -1 \\
\end{array}\right]\end{displaymath}](img497.gif)
![\begin{displaymath}A'=\left[
\begin{array}{cccc}
1 & 2 & 0 & 0 \\
0 & 0 & 1 ...
...\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & -1 \\
\end{array}\right]\end{displaymath}](img498.gif)
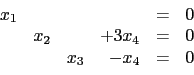
最後我們說明一下, 雖然一個矩陣化為 echelon form 的情形不唯一, 不過我們可以利用 Proposition 2.3.3 的結果證明一個矩陣化為 reduced echelon form 的結果會唯一. 然而這個事實我們以後不會用到, 這裡就略去不證了.