next up previous
下一頁: 中的向量 上一頁: Vectors 前一頁: Vectors

二維平面中的向量

本節針對對抽象數學論述不熟悉的同學, 想利用大家熟悉坐標平面的向量慢慢引導進入狀況. 也因此本節在細節的說明特別繁瑣. 若對坐標平面的向量相當清楚的同學, 可放心略過此節.

在坐標平面中的向量, 我們都可用 $ (a,b)$ 來表示, 其中 $ a,b\in\mathbb{R}$ (我們用 $ \mathbb{R}$ 來表示所有實數所成的集合, 所以 $ a,b\in\mathbb{R}$ 表示 $ a,b$ 屬於實數, 也就是說 $ a,b$ 皆為實數). 意思就是說如果你在坐標平面中任給一點 $ P$, 然後從 $ P$ 點開始往水平方向走 $ a$ 單位 ($ a>0$ 時往右; $ a<0$ 時往左), 再沿鉛直方向走 $ b$ 單位 ($ b>0$ 時往上; $ b<0$ 時往下), 最後到達的點若記為 $ Q$. 那麼從 $ P$ 點開始到 $ Q$ 點為止的這一個向量就可用 $ (a,b)$ 來表示, 記為 $ \overrightarrow{PQ}=(a,b)$.

用坐標來表示一個向量 (即用 $ (a,b)$ 這種方法) 有許多好處, 例如大家很容易理解: 當兩個向量 $ (a,b)$ 和 $ (c,d)$ 相等時 (即 $ (a,b)=(c,d)$), 這表示 $ a=c$ 且 $ b=d$; 從這觀點若用點來表示向量時就較麻煩, 因為如果 $ P,P',Q,Q'$ 為平面中四個點 $ \overrightarrow{PQ}=\overrightarrow{P'Q'}$ 並不代表 $ P$ 和 $ P'$ 為同一點且 $ Q$ 和 $ Q'$ 為同一點. 不過若已知 $ P=P'$ , 則可得 $ Q=Q'$. 反之若 $ Q=Q'$ 則可得 $ P=P'$. (我們說明一下這裡符號的使用: 因為 $ P,P'$ 皆為``點''而不是``數'', 所以這裡 $ P=P'$ 這個等號表示同一``點''而不是同一``數''). 上面這個論述可用剛才定義 $ \overrightarrow{PQ}$ 的方法驗證, 這裡就不再驗證. 基於符號的方便性, 當我們要用符號來表示一個向量時, 除非已知此向量為特定兩點所決定的向量, 通常會僅用 $ \mathbf{u},\mathbf{v}$ 這類的粗體字符號來表示. 一般來說我們用 $ \mathbb{R}^2$ 來表示坐標平面上的向量所成的集合, 所以若我們說 $ \mathbf{v}\in\mathbb{R}^2$, 就表示 $ \mathbf{v}$ 是坐標平面上的一個向量, 也就是說可以找到 $ a,b\in\mathbb{R}$ 使得 $ \mathbf{v}=(a,b)$.

坐標表示法的另一個好處是很容易幫助我們定義向量的加法 (addition) 以及係數積 (scalar multiplication).

Definition 1.1.1   令 $ \mathbf{u}=(a_1,a_2),\mathbf{v}=(b_1,b_2)\in\mathbb{R}^2$ 以及 $ r\in\mathbb{R}$. 我們定義

$\displaystyle \mathbf{u}+\mathbf{v}=(a_1+b_1,a_2+b_2)\quad\mathrm{and}\quad r\mathbf{u}=(ra_1,ra_2).$

要注意這裡所謂的定義 (即 definition) 指的是規定, 也就是說我們規定向量必須這樣相加及乘上一個常數. 當然了你也可以自行規定一套向量加法的規則. 不過一般在數學上的定義都有其必要性, 通常一個定義對理論推導或實用上都會有相當的幫助. 例如這一個定義與我們直觀上認為若 $ P,Q,R$ 為坐標平面上三點, 則 $ \overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PR}$ 相吻合. 這是因為: 假設 $ P,Q,R$ 三點的坐標分別為 $ P(x_1,y_1), Q(x_2,y_2), R(x_3,y_3)$ (注意: 為了區分點和向量的坐標表示法, 當我們提到點的坐標時都會加上該點的代號), 則

$\displaystyle \overrightarrow{PQ}=(x_2-x_1,y_2-y_1), \overrightarrow{QR}=(x_3-x_2,y_3-y_2), \overrightarrow{PR}=(x_3-x_1,y_3-y_1).$

然而依前面向量加法的定義確實

$\displaystyle \overrightarrow{PQ}+\overrightarrow{QR}=\left((x_2-x_1)+(x_3-x_2),(y_2-y_1)+(y_3-y_2)\right)=\left(x_3-x_1,y_3-y_1\right).$

故得

$\displaystyle \overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PR}.$ (1.1)

一個定義一定要清楚明確, 例如若 $ \mathbf{u}=(1,2),\mathbf{v}=(3,4)$ 且 $ r=5$, 由 Definition 1.1.1 我們知 $ \mathbf{u}+\mathbf{v}=(1+3,2+4)=(4,6)$ 且 $ r\mathbf{u}=(5\times 1, 5\times 2)=(5,10)$. 不過我們決不能用: 若 $ \mathbf{u}=(1,2),\mathbf{v}=(3,4)$ 且 $ r=5$, 則定義 $ \mathbf{u}+\mathbf{v}=(1+3,2+4)=(4,6)$ 且 $ r\mathbf{u}=(5\times 1, 5\times 2)=(5,10)$ 這樣的說法來定義向量的加法及係數積. 因為這樣的說法只是定義出兩個特殊的向量的加法以及和一特殊實數的乘積, 不能依這特例要求別人``依此類推''. 這就是當初定義時用 $ a_1,a_2,b_1,b_2,r$ 這些符號來代替具體數字的用意. 另外要注意在 Definition 1.1.1 中我們沒有提 $ r\mathbf{v}$ 的定義, 不過當初既然 $ \mathbf{u}$ 已表成任意 $ \mathbb{R}^2$ 上的向量, 定義 $ r\mathbf{u}$ 已足夠所以不必再去定 $ r\mathbf{v}$. 最後要強調的是: 這裡我們並沒有定義兩向量的乘法, 而是定義實數和向量相乘, 所以我們稱為係數積 (scalar multiplication) 而不能說是向量的乘法.

有了定義之後, 我們就需依定義處理相關問題, 但通常直接依定義處理較繁複, 我們可依定義推導出一些性質, 利用這些性質簡化處理程序. 例如在微積分, 我們定義出一個函數在某一點的極限後, 若每次都得依定義處理極限問題論證起來很複雜; 但當我們利用定義推導出一些極限的性質後, 用這些性質處理極限問題就簡單方便多了. 所以在定義之後我們會有一些定理 (Proposition 或 Theorem) 來論證一些依定義可得的性質, 以方便我們處理更進一步的問題. 以下就是要談向量加法及係數積有關的性質.

Proposition 1.1.2   對於 $ \mathbb{R}^2$ 上的向量, 我們有以下的性質:
  1. 對任意 $ \mathbf{u},\mathbf{v}\in\mathbb{R}^2$, 皆有 $ \mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u}$.
  2. 對任意 $ \mathbf{u},\mathbf{v}, \mathbf{w}\in\mathbb{R}^2$, 皆有 $ (\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w})$.
  3. 存在一向量 $ \mathbf{0}\in\mathbb{R}^2$ 滿足對任意 $ \mathbf{u}\in\mathbb{R}^2$ 皆有 $ \mathbf{0}+\mathbf{u}=\mathbf{u}$.
  4. 對任意 $ \mathbf{u}\in\mathbb{R}^2$ 皆可找到 $ \mathbf{u'}\in\mathbb{R}^2$ 滿足 $ \mathbf{u}+\mathbf{u'}=\mathbf{0}$.
  5. 對任意 $ r,s\in\mathbb{R}$ 以及 $ \mathbf{u}\in\mathbb{R}^2$, 皆有 $ r(s\mathbf{u})=(rs)\mathbf{u}.$
  6. 對任意 $ r,s\in\mathbb{R}$ 以及 $ \mathbf{u}\in\mathbb{R}^2$, 皆有 $ (r+s)\mathbf{u}=r\mathbf{u}+s\mathbf{u}.$
  7. 對任意 $ r\in\mathbb{R}$ 以及 $ \mathbf{u},\mathbf{v}\in\mathbb{R}^2$ 皆有 $ r(\mathbf{u}+\mathbf{v})=r\mathbf{u}+r\mathbf{v}$.
  8. 對任意 $ \mathbf{u}\in\mathbb{R}^2$, 皆有 $ 1\mathbf{u}=\mathbf{u}$.

通常一個定理敘述完就要證明, 不過在這裡我們建議先緩一緩. 對同學來說了解定理說些什麼比起證明來得重要. 在這裡我們就一一說明一下這個定理說些什麼.

(1) 敘述的是所謂向量加法的交換性. 它告訴我們在處理向量加法時可以依方便交換順序. 或許同學覺得這個很自然為何還要證明. 事實上只要是定義未提的事情都要證明, 不能因為覺得自然而不去處理. 這裡大家會覺得自然是因為大家對實數的加法運算很清楚, 不過數學上是存在許多``抽象''的數系它的加法是不能交換的. 所以經由證明不只讓我們確認事情是對的, 也能幫助我們釐清事情是對的其背後的主要因素.

(2) 說的就是所謂的結合律, 它依然是因為實數加法的性質而成立. 這裡 $ (\mathbf{u}+\mathbf{v})+\mathbf{w}$ 是說先將 $ \mathbf{u}$ 和 $ \mathbf{v}$ 相加後所得的向量再和 $ \mathbf{w}$ 相加. 這樣所得的向量和先將 $ \mathbf{v}$ 和 $ \mathbf{w}$ 相加後再和 $ \mathbf{u}$ 相加會是同樣的向量. 這裡雖然也是談向量加法的順序問題, 不過和 (1) 所談的順序是兩回事, 大家應該要分清楚.

(3) 談的就是所謂的零向量, 零向量的特點就是加上任何向量都不動. 為什麼要特別談零向量的存在性? 這就好比在實數上若沒有零的概念就沒有減法一樣, 在向量的運算上是相當重要的. 尤其以後要用抽象的方式談向量系統時零向量的存在性更不容忽視.

(4)談的就是所謂的反向量, 要注意需有零向量的存在才能談反向量. 而且要區分清楚這裡的敘述是給了 $ \mathbf{u}$ 後可找到 $ \mathbf{u'}$ 使得 $ \mathbf{u}+\mathbf{u'}=\mathbf{0}$. 這裡 $ \mathbf{u'}$ 是會隨著 $ \mathbf{u}$ 而改變, 而不是一個固定的向量和所有的向量加起來會是零向量. 數學的敘述要弄清楚否則差之毫釐失之千里.

(5),(6),(7) 談的是係數積的性質, 例如 $ r(s\mathbf{u})$ 表示是先將 $ \mathbf{u}$ 乘上 $ s$ 倍後所得的向量再乘上 $ r$. 這幾個性質也都和實數乘法性質息息相關, 雖然 看起來不顯眼但在處理向量的運算時非常重要.

(8) 指的是所有向量乘上 $ 1$ 後仍不動. 這裡特別提出來其實和零向量意義很像, 唯有 $ 1$ 的引入以後才能談係數的除法. 例如已知 $ 2\mathbf{u}=\mathbf{v}$, 就可利用 (5) 的性質兩邊乘上 $ 1/2$, 得

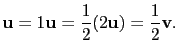
$\displaystyle \mathbf{u}=1\mathbf{u}=\frac{1}{2}(2\mathbf{u})=\frac{1}{2}\mathbf{v}.$

最後要強調一下: 這裡將這些性質列出, 並不是要求大家將這幾個性質背下來. 一來我們希望大家知道有些性質不能覺得理所當然就不去證明, 另一方面也讓大家知道以後在處理向量運算時可以放心且自然的使用這幾個性質. 現在我們就來看看這些證明.

証 明. (of Proposition 1.1.2) 這幾個性質其實很簡單, 我們寫下證明是希望不熟悉寫抽象證明的同學利用這個簡單的證明學學看如何寫好證明. 若自覺對這些性質的證明清楚的同學可跳過此證明.
  1. 假設 $ \mathbf{u}=(a_1,a_2),\mathbf{v}=(b_1,b_2)$, 則依定義知

    $\displaystyle \mathbf{u}+\mathbf{v}=(a_1+b_1,a_2+b_2),\, \mathbf{v}+\mathbf{u}=(b_1+a_1,b_2+a_2).$

    故由實數加法的交換性 (即 $ a+b=b+a$) 可得 $ \mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u}$.

  2. 假設 $ \mathbf{u}=(a_1,a_2),\mathbf{v}=(b_1,b_2),\mathbf{w}=(c_1,c_2)$, 則依定義知 $ \mathbf{u}+\mathbf{v}=(a_1+b_1,a_2+b_2)$ 故得

    $\displaystyle (\mathbf{u}+\mathbf{v})+\mathbf{w}=((a_1+b_1)+c_1,(a_2+b_2)+c_2).$

    同理由 $ \mathbf{v}+\mathbf{w}=(b_1+c_1,b_2+c_2)$ 可得

    $\displaystyle \mathbf{u}+(\mathbf{v}+\mathbf{w})=(a_1+(b_1+c_1),a_2+(b_2+c_2)).$

    因此由實數加法的結合律 (即 $ (a+b)+c=a+(b+c)$) 得知 $ (\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{v}+(\mathbf{u}+\mathbf{w})$.

  3. 這是一個存在性的問題, 也就是說要找到一個向量 $ \mathbf{0}$ 滿足所求. 這裡我們只要令 $ \mathbf{0}=(0,0)$, 則對任意向量 $ \mathbf{u}=(a_1,a_2)$ 皆有

    $\displaystyle \mathbf{0}+\mathbf{u}=(0+a_1,0+a_2)=(a_1,a_2)=\mathbf{u}.$

    故知確實存在這樣的向量.

  4. 上面我們已知可令 $ \mathbf{0}=(0,0)$, 故此時對任意 $ \mathbf{u}=(a_1,a_2)$ 我們只要考慮 $ \mathbf{u'}=(-a_1,-a_2)$, 則可得

    $\displaystyle \mathbf{u}+\mathbf{u'}=(a_1+(-a_1),a_2+(-a_2))=(0,0)=\mathbf{0}.$

  5. 假設 $ \mathbf{u}=(a_1,a_2)$, 依定義知 $ s\mathbf{u}=(sa_1,sa_2)$, 因此得

    $\displaystyle r(s\mathbf{u})=(r(sa_1),r(sa_2)).$

    另一方面

    $\displaystyle (rs)\mathbf{u}=((rs)a_1,(rs)a_2),$

    故由實數乘法結合律 (即 $ r(sa)=(rs)a$) 可得 $ r(s\mathbf{u})=(rs)\mathbf{u}.$

  6. 假設 $ \mathbf{u}=(a_1,a_2)$, 依定義知

    $\displaystyle (r+s)\mathbf{u}=((r+s)a_1,(r+s)a_2).$

    另一方面 $ r\mathbf{u}=(ra_1,ra_2),s\mathbf{u}=(sa_1,sa_2)$, 可得

    $\displaystyle r\mathbf{u}+s\mathbf{u}=(ra_1+sa_1,ra_2+sa_2),$

    故由實數加法與乘法的分配律 (即 $ (r+s)a=ra+sa$) 可得 $ (r+s)\mathbf{u}=r\mathbf{u}+s\mathbf{u}.$

  7. 假設 $ \mathbf{u}=(a_1,a_2),\mathbf{v}=(b_1,b_2)$, 依定義知

    $\displaystyle r(\mathbf{u}+\mathbf{v})=(r(a_1+b_1),r(a_2+b_2)).$

    另一方面 $ r\mathbf{u}=(ra_1,ra_2),r\mathbf{v}=(rb_1,rb_2)$, 可得

    $\displaystyle r\mathbf{u}+r\mathbf{v}=(ra_1+rb_1,ra_2+rb_2),$

    故由實數加法與乘法的分配律 (即 $ r(a+b)=ra+rb$) 可得 $ r(\mathbf{u}+\mathbf{v})=r\mathbf{u}+r\mathbf{v}$.

  8. 假設 $ \mathbf{u}=(a_1,a_2)$, 由於對任意實數 $ a$ 皆有 $ 1a=a$, 故由 $ 1\mathbf{u}=(1a_1,1a_2)$ 可得 $ 1\mathbf{u}=\mathbf{u}.$
$ \qedsymbol$

接下來我們將舉一個例子來說明我們可以用向量的性質 (Proposition 1.1.2) 來處理一些幾何的問題. 由於這些性質以後我們不會用到, 所以在此不用定理的形式呈現而是用例題的形式呈現.

Example 1.1.3   假設 $ P,Q,R,S$ 是平面中四個點, 其中 $ \overrightarrow{PQ}=\overrightarrow{SR}$, 則我們有以下性質:
  1. $ \overrightarrow{QR}=\overrightarrow{PS}$.
  2. 假設 $ T$ 為線段 $ \overline{PR}$ 和線段 $ \overline{SQ}$ 的交點, 則 $ \overrightarrow{PT}=\overrightarrow{TR}$ 且 $ \overrightarrow{ST}=\overrightarrow{TQ}$.

我們利用下圖來解釋這兩個性質會成立的原因:


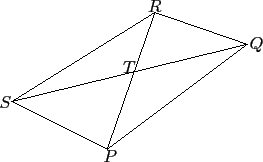
\begin{picture}(160,100)(0,0) \thinlines\drawpath{68.0}{8.0}{156.0}{74.0} \drawp... ...rawcenteredtext{4.0}{38.0}{$S$} \drawcenteredtext{82.0}{60.0}{$T$} \end{picture}

  1. 我們要利用 $ \overrightarrow{PQ}=\overrightarrow{SR}$ 來得到 $ \overrightarrow{QR}=\overrightarrow{PS}$. 由前面式子 (1.1) 我們知道 $ \overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PR}$ 且 $ \overrightarrow{PS}+\overrightarrow{SR}=\overrightarrow{PR}$. 也就是說

    $\displaystyle \overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PS}+\overrightarrow{SR}.$ (1.2)

    由 Proposition 1.1.2 (4), 我們知存在 $ \mathbf{u}$ 使得 $ \overrightarrow{PQ}+\mathbf{u}=\mathbf{0}$. 要注意由於 Proposition 1.1.2 (1) 以及 $ \overrightarrow{PQ}=\overrightarrow{SR}$ 的假設, 這等於

    $\displaystyle \overrightarrow{PQ}+\mathbf{u}=\mathbf{u}+\overrightarrow{PQ}=\overrightarrow{SR}+\mathbf{u}=\mathbf{u}+\overrightarrow{SR}=\mathbf{0}$

    現將上面式子 (1.2) 兩邊加上 $ \mathbf{u}$ 可得

    $\displaystyle \mathbf{u}+(\overrightarrow{PQ}+\overrightarrow{QR})=\mathbf{u}+(\overrightarrow{PS}+\overrightarrow{SR})$ (1.3)

    然而利用 Proposition 1.1.2 (2), (3) 我們有

    $\displaystyle \mathbf{u}+(\overrightarrow{PQ}+\overrightarrow{QR})=(\mathbf{u}+... ...ow{PQ})+\overrightarrow{QR}=\mathbf{0}+\overrightarrow{QR}=\overrightarrow{QR}.$

    同理可得

    $\displaystyle \mathbf{u}+(\overrightarrow{PS}+\overrightarrow{SR})=(\overrighta... ...rrightarrow{SR}+\mathbf{u})=\overrightarrow{PS}+\mathbf{0}=\overrightarrow{PS}.$

    故由式子 (1.3) 可得 $ \overrightarrow{QR}=\overrightarrow{PS}$.

  2. 通常我們用坐標來處理問題時, 碰到交點的問題可以用解方程式的方法處理, 不過這裡我們要用抽象的向量處理, 遇到交點問題就比較麻煩, 需要用比較特殊的方法處理. 這裡原要證明線段 $ \overline{PR}$ 和線段 $ \overline{SQ}$ 的交點會是 $ \overline{PR}$ 以及 $ \overline{SQ}$ 的中點. 我們用反過來的看法處理, 也就是要去說明 $ \overline{PR}$ 的中點和 $ \overline{SQ}$ 的中點會是同一點. 如此一來這一點因同時在 $ \overline{PR}$ 和 $ \overline{SQ}$ 上, 所以自然就是 $ \overline{PR}$ 和 $ \overline{SQ}$ 的交點. 又因為 $ \overline{PR}$ 和 $ \overline{SQ}$ 不平行, 僅能有一個交點, 這就說明了線段 $ \overline{PR}$ 和線段 $ \overline{SQ}$ 的交點就是 $ \overline{PR}$ 以及 $ \overline{SQ}$ 的中點. 具體來說我們假設 $ T',T''$ 分別為 $ \overline{PR}$ 和 $ \overline{SQ}$ 的中點. 然後說明 $ T'=T''$, 如此一來便得證 $ T'$ 為 $ \overline{PR}$ 和 $ \overline{SQ}$ 的交點, 也就是說 $ T=T'=T''$, 故得證所求.

    依假設 $ T',T''$ 分別為 $ \overline{PR}$ 和 $ \overline{SQ}$ 的中點, 故知

    $\displaystyle \overrightarrow{PT'}=\overrightarrow{T'R}=\frac{1}{2}\overrightarrow{PR}$ (1.4)

    且

    $\displaystyle \overrightarrow{ST''}=\overrightarrow{T''Q}=\frac{1}{2}\overrightarrow{SQ}.$ (1.5)

    若我們能證明 $ \overrightarrow{PT'}=\overrightarrow{PT''}$ 便得證 $ T'=T''$. 然而 $ \overrightarrow{PT''}=\overrightarrow{PS}+\overrightarrow{ST''}$, 故由式子 (1.5) 可得

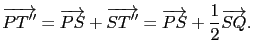
    $\displaystyle \overrightarrow{PT''}=\overrightarrow{PS}+\overrightarrow{ST''}=\overrightarrow{PS}+\frac{1}{2}\overrightarrow{SQ}.$

    又由於 (1) 告訴我們 $ \overrightarrow{PS}=\overrightarrow{QR}$ 上式可改寫為

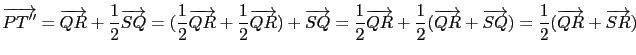
    $\displaystyle \overrightarrow{PT''}=\overrightarrow{QR}+\frac{1}{2}\overrightar... ...w{QR}+\overrightarrow{SQ})=\frac{1}{2}(\overrightarrow{QR}+\overrightarrow{SR})$

    再利用已知 $ \overrightarrow{PQ}=\overrightarrow{SR}$, 上式又可改寫為

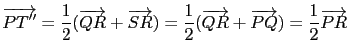
    $\displaystyle \overrightarrow{PT''}=\frac{1}{2}(\overrightarrow{QR}+\overrighta... ...c{1}{2}(\overrightarrow{QR}+\overrightarrow{PQ})=\frac{1}{2}\overrightarrow{PR}$

    故由式子 (1.4) 得證 $ \overrightarrow{PT'}=\overrightarrow{PT''}$, 也因此得知 $ T'=T''$ 就是 $ \overline{PR}$ 和 $ \overline{SQ}$ 的交點, 也就是說 $ T=T'=T''$. 故由式子 (1.4,1.5) 得證 $ \overrightarrow{PT}=\overrightarrow{TR}$ 且 $ \overrightarrow{ST}=\overrightarrow{TQ}$.

同學或許會想到用設定坐標的方式處理 Example 1.1.3 的問題. 這裡我們故意不去設定坐標系, 而僅用 Proposition 1.1.2 中列出的向量運算性質去處理, 主要就是要強調這幾個運算性質就足以處理向量有關的性質. 也就是說不一定需要架設坐標系, 只要符合 Proposition 1.1.2 中列出的運算性質, 都可享有 Example 1.1.3 的性質. 另外由 Example 1.1.3 的處理過程中我們了解到, Proposition 1.1.2 的運算性質可幫助我們在處理向量有關的等式運算時可如處理實數的等式運算一樣 (例如移項, 消去...等). 這些等我們以後更進一步談向量空間時, 大家就更能體會了.

next up previous
下一頁: 中的向量 上一頁: Vectors 前一頁: Vectors
Cellist 2010-12-08