2. SAS

即知道兩邊長及其夾角 (本題就是這樣的情況), 也就是說我們知道兩邊 a, c 以及夾角 B 之值或是 b, a 及 C 或是 c, b 及 A 之值. 我們舉知道 a, c, B 為例, 此時利用餘弦定理馬上知道 b = $\sqrt{a^2+c^2-2ac\cos B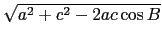}$. 既然知道 a, b, c 之值了, 我們就可回到 SSS 的情形(用餘弦定理)求出另外兩個角 A, C. 要注意, 一開始處理 SAS 的情形時, 正弦定理幾乎派不上用場. 不過在求得第三邊後, 我們就可利用正弦定理求得各角的正弦值. 例如我們目前處理的情形(即知道 a, c, B 之值), 求出 b 值後我們就可利用正弦求出 sin A = (a/b)sin B 以及 sin C = (c/b)sin B. 這裡由於我們知道其中一個角為何, 所以不像單純的 SSS 之情形僅得 sin A, sin B, sin C 之比值, 而是正確的求出它們的值. 這個看法對處理這一題很有幫助.