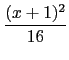4

坐標平面上方程式 ${\dfrac{x^2}{9}}$ + ${\dfrac{y^2}{4}}$ = 1 的圖形與 ${\dfrac{(x+1)^2}{16}}$ - ${\dfrac{y^2}{9}}$ = 1 的圖形共有幾個交點？

(1) 1 個         (2) 2 個         (3) 3 個         (4) 4 個         (5) 0 個

說明:求交點個數問題可以用代數方法, 即解方程式求解的個數; 也可以用幾何方法處理. 這裡由於方程式是二次曲線標準形式(或僅經平移), 出題者應該是傾向希望用幾何方法, 考橢圓和雙曲線的基本性質.

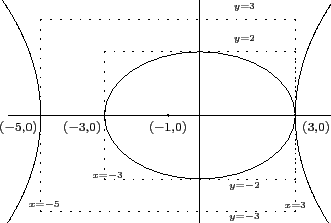
若用代數解方程式處理, 由於 x² 和 x 項皆有出現, 而 y 僅出現 y²項, 所以應將 y 換成 x. 也就是將 y² = 4(1 - (x²/9)) 代入另一式解 x, 得 x = 3 或 x = - 597/145. 當 x = 3 時得 y = 0 (重根). 而當 x = - 597/145 時因 x < - 3, 得 y 為虛數. 故知僅有一個交點. 此解法計算繁複故不推薦.

若是用幾何的方法, 此題變成比較知識性的問題, 知道一個是橢圓另一個是雙曲線, 然後利用方程式把幾個重要的資訊列出就可畫圖或簡單分析求出交點個數了. 首先橢圓的中心在 (0, 0), 長軸在 x 軸且半長軸長為 3, 又半短軸長為 2. 因此知橢圓的頂點為 (±3, 0), (0,±2), 且橢圓在 x = ±3 和 y = ±2 這四條線所圍的區域內. 另一個曲線為雙曲線, 其中心在 (- 1, 0), 貫軸在x 軸且半貫軸長為 4, 又半共軛軸長為 3. 所以雙曲線的頂點分別為 (3, 0) 和 (- 5, 0), 且雙曲線會在 x = 3 和 x = - 5 這兩條直線的外部, 如下圖所示. 故知此二曲線僅相交於 (3, 0) 這一點.