5

關於坐標平面上函數 y = sin x 的圖形和 y = ${\dfrac{x}{10\pi}}$ 的圖形之交點個數，下列哪一個選項是正確的？

(1) 交點的個數是無窮多                     (2) 交點的個數是奇數且大於 20

(3) 交點的個數是奇數且小於 20         (4) 交點的個數是偶數且大於或等於 20

(5) 交點的個數是偶數且小於 20

說明:又一個求交點個數問題, 不過本題因為有一個三角函數不是多項式, 無法用代數解方程式的方法求解. 選項並沒有要求精確地算出交點個數, 看起來好像可以用這些函數的特性估計交點個數, 不過事實上仍是要精確的算出個數才能選答. 不很清楚出題者為何要用這些選項, 而不直接用選填題方式. 或許出題者想分辨出誤以為會有無窮多個交點的同學, 不過這是單選題, 即使知道不會有無窮多個交點但是算錯了, 還是和誤以為有無窮多點的同學一樣沒有辦法被分辨出來.

若僅是問交點個數是否有限, 或問交點個數為奇數或偶數, 很容易由 y = sin x 是有界的以及其週期性, 還有 y = sin x 和 y = x/(10$\pi$) 對原點的對稱性知道是有限且為奇數. 不過又要回答交點個數是否大於等於 20, 就得更精細判斷了, 也就是說我們必須對 y = sin x 這一個函數充分的了解. 首先我們判斷有可能有交點的範圍. 因為 -1$\le$sin x$\le$1, 所以 y = x/(10$\pi$) 只能在 -1$\le$x/(10$\pi$)$\le$1 (即 -10$\pi$$\le$x$\le$10$\pi$) 時會和 y = sin x 相交. 所以同學可以在 -10$\pi$$\le$x$\le$10$\pi$ 之間大致畫出 y = sin x 的函數圖形, 再畫出 (- 10$\pi$, - 1) 與 (10$\pi$, 1) 這兩點連線 (即直線 y = x/(10$\pi$)), 就可算出共交 19 點. 這裡我們說的很模糊, 因為如果要說清楚, 可能弄得同學們更糊塗. 說穿了, 就是在高中數學中我們只能告訴學生 y = sin x 長什麼樣子, 並不能很清楚地描繪其上升下降的陡峭情形, 所以此題若要精確的算出有幾個交點, 嚴格說起來不是很合理.

讓我們嘗試著把事情說清楚. 由於 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形皆對原點對稱 (即若 (a, b) 在圖形上, 則 (- a, - b) 亦在圖形上), 所以我們只要算清楚 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形在 0$\le$x$\le$10$\pi$ 的相交情形, 另一半就可輕鬆解決. 在這種情形時我們發現 y = x/(10$\pi$) 是在原點由高度 y = 0 依一定的傾斜度``慢慢地''(請容許我們用慢慢地這種字眼)爬升, 最後在 x = 10$\pi$ 時到達 y = 1 這樣的高度 (即 (10$\pi$, 1) 這一點). 而 y = sin x 則是每當 x 分別在

$${\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}}$$ (96.1)

時由 y = 0 ``快快地''爬升到 y = 1 這樣的高度. 另一方面每當 x 分別在

$${\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi \pi {\frac{\pi}{2}} \pi$$ (96.2)

時, y = sin x 又由 y = 1 降回到 y = 0. 當 x $\in$ [0, 10$\pi$] 在 (96.1) 和 (96.2) 這些區間以外的情況, 由於 y = sin x < 0 在 x 軸下方, 不可能與 y = x/(10$\pi$) 相交, 所以我們只要算 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形在 (96.1) 和 (96.2) 這些區間相交的個數即可.

當 x 在 (96.1) 和 (96.2) 這些區間的端點時 f (x) = sin x - x/(10$\pi$) 的取值皆異號 (除了 x = 0 時, f (0) = 0), 所以利用連續函數的勘根定理我們知 f (x) 在這些區間皆有根, 也就是說 y = sin x 和 y = 1/(10$\pi$) 在這些區間必相交. 所以我們知在 x$\ge$ 0 時 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形至少相交 10 次. 利用對稱性知 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形在 x$\le$ 0 時也至少相交 10 次. 不過要注意在 x $\in$ [0,${\frac{\pi}{2}}$] 這個區間, 交點是在 (0, 0), 這一點分別在算 x$\ge$ 0 和 x$\le$ 0 時都有被算到, 所以計算合起來的交點數時需扣掉多算的一次, 故得 y = sin x 和 y = x/(10$\pi$) 這兩個函數圖形至少相交 10 + 10 - 1 = 19 次. 算到這部份仍沒有超出高中課程範圍, 所以此題若選項分段是在 19 而不是 20, 會比較合理.

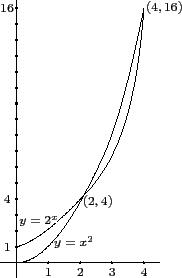
既然已知交點數是奇數, 而題目是由 20 分界, 由前面算出的結果我們無法知要選 (2) 還是 (3), 所以還必須更精確地算下去. 當 x 在 (96.2) 這些區間時, 我們很容易知道兩函數僅交 1 點, 因為在這些區間 y = x/(10$\pi$) 是上升的而 y = sin x 是下降的, 不可能在相交後又拐回來再碰一次. 當 x 在 (96.1) 這些區間時就比較麻煩了, 此時兩個函數都是上升的, 除非對它們上升速度的改變 (這牽涉到二次導函數) 相當了解, 否則很難精確知道它們相交的個數. 這裡我們舉一個常見的例子: y = x² 和 y = 2^x 這兩個函數的圖形. 它們相交的情形如下圖. 請注意, 此圖只是為了要描繪這兩函數相交的情形, 它並不是很精確的函數圖形.

在 x$\ge$ 0 時, 這兩個函數圖形都是上升的. 而當 0$\le$x$\le$2 時, y = x² 的圖形由 y = 0 ``快快''爬升到 y = 4. 此時 y = 2<sup>x</sup> 的圖形由 y = 1 以較緩和的方式爬升到 y = 4, 在這個區間兩函數交於 (2, 2) 這一點. 接下來兩個函數並不是從此說``拜拜''而不再相交. 在 2$\le$x$\le$4 時, y = x² 的圖形由 y = 4 爬升到 y = 16. 但此時 y = x² 的圖形雖在 y = f (x) 的下方卻以更快更陡的方式由 y = 4 爬升到 y = 16, 在這個區間兩函數再次交於 (4, 16). 之後才因 y = 2^x 爬升的速度都比 y = x² 快, 所以兩函數圖形不再相交. 由此可知, 當兩個函數圖形都是向上爬升時, 是很難預期它們相交的情形.

現在讓我們回到主題, 當 x 在 (96.1) 這幾個區間時, 一開始雖然 y = sin x 的圖形在 y = x/(10$\pi$) 的下方, 但 y = sin x 是以``較快''的速度上升, 所以會趕上而碰到 y = x/(10$\pi$). 接下來當然 y = sin x 跑到 y = x/(10$\pi$) 的上方, 但它們有沒有可能在 y = sin x 開始下降之前再次相遇呢? 其實 y = sin x 雖然一開始比 y = x/(10$\pi$) 陡的方式上升, 但它陡的情形是越來越緩和 (這樣最後才會下降), 而 y = x/(10$\pi$) 卻是一直以一定的傾斜度上升. 所以當 y = sin x 爬到 y = x/(10$\pi$) 上方時, 一段時間後 y = x/(10$\pi$) 確實有比 y = sin x 更快速地在攀升, 但在 y = sin x 下降之前都無法趕上 y = sin x. 這是因為若在 y = sin x 下降之前 y = x/(10$\pi$) 趕上 y = sin x 而與之相交, 此時由於 y = x/(10$\pi$) 的上升的傾斜度都比 y = sin x 上升的傾斜度陡 (別忘了 y = sin x 上升的傾斜度一直在下降), 會造成 y = sin x 的圖形在 y = x/(10$\pi$) 圖形的下方, 永遠無法趕上 y = x/(10$\pi$) 與之再次相交. 但我們知當 y = sin x 在下降後 (即 x 在 (96.2) 那些區間) 是會和 y = x/(10$\pi$) 相交的, 故由此矛盾知當 x 在 (96.1) 這幾個區間時 y = sin x 一旦與 y = x/(10$\pi$) 相交後就不會再相交, 所以在這些區間中每次僅相交一次.

當 x 在 (96.1) 和 (96.2) 這些區間 (即在 [0,$\pi$], [2$\pi$, 3$\pi$], [4$\pi$, 5$\pi$], [6$\pi$, 7$\pi$], [8$\pi$, 9$\pi$] 這些區間) y = sin x 的圖形從上升但越來越緩和慢慢變成下降且越降越快, 這樣的圖形我們稱為``凹向下''圖形. 一般來說一個函數在一個區間為凹向下時, 其圖形與直線在這個區間最多只能交兩點, 上面就是在解釋這個現象. 也就是說當 x 在上述五個區間時, y = sin x 至多只能和 y = x/(10$\pi$) 交於 10 點, 所以結合前面所知 (即至少交於 10 點) 便能精確的算出它們的交點數.

y = sin x 的圖形相信同學們都知道, 但是前面所提的這``凹向下"的性質, 在高中教材中卻未見. 雖然畫一畫圖是能感受其和直線相交情形, 但是筆者仍認為選項分段分在 19 就足以分辨出學生對 y = sin x 圖形的理解程度.