


�U�@��: Subring
�W�@��: ��� Ring ���ʽ�
�e�@��: �� Ring ���w�q�ұo���ʽ�
�ڭ̤w�g���D�@�� ring �������N�������W 0 ���� 0, ���L�b�@�몺
ring �����i��s�b��Ӥ����� 0 �������ۭ��H�ᵥ�� 0. �t� �b�@�몺
ring �����i��Ǥ����S�����k�� inverse, �ҥH�����k inverse
�������N��o�ܯS�O�F. �b�o�@�`���ڭ̱N�Q�׳o��دS�O������.
Definition 5.3.1
�O
R �O�@�� ring. �p�G
a
0 �O
R ���@�Ӥ����B�b
R ���s�b
b
0 �ϱo
a . b = 0 ��
b . a = 0, �h��
a �O
R ���@��
zero-divisor.
���M�F�b�w�q�̪� b �]�O R �� zero-divisor.
Example 5.3.2
�۫H�j�a���ܤF��
�o�@�� abelian group.

+
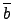
�����ȬO��
a +
b ���H 6
���l��. �Ҧp
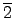
+
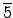
=
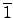
. �ۦP���ڭ̤]�i�H�b

/6

���w�@�ӭ��k.
 .
. 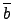
���ȴN�O
a . b ���H 6
���l��. �Ҧp
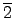 .
. 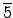
=
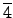
.
�j�a�ܮe���ˬd�b�o�˪��[�k�M���k���U

/6

�O�@�� ring. �䤤

�O

/6

�� 0 (�[�k�� identity). �]��
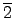


�B
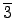


, ��
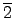 .
. 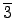
=

. �G�ѩw�q��
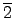
�M
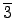
�O

/6

�� zero-divisor. �S�]
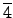 .
. 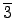
=

, �ҥH
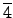
�]�O zero-divisor. �t� �ڭ̥i�H�ˬd
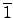
�M
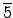
���W������

�����������|����

, �ҥH�ڭ̪�
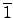
�M
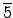
�����O

/6

�� zero-divisor.
�� a �O�@�� zero-divisor ��, �ܤ��n���Ʒ|�o��: �N�O�ܥi��
a . x = a . y ���O x y (�άO
x . a = y . a ���O x
y (�άO
x . a = y . a ���O x y).
�Ҧp�b
y).
�Ҧp�b
 /6
/6 ���ڭ̤����o�
���ڭ̤����o�
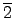 .
. 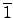 =
= 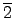 .
. 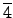 =
= 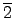 . �|�ɭP�o�˪��O�o�ͬO�]���Y a �O
zero-divisor, ���] b
. �|�ɭP�o�˪��O�o�ͬO�]���Y a �O
zero-divisor, ���] b 0 ����
a . b = 0 (��
b . a = 0). �h
0 ����
a . b = 0 (��
b . a = 0). �h
a . (b + c) = a . b + a . c = 0 + a . c = a . c
(��
(b + c) . a = b . a + c . a = 0 + c . a = c . a),
���O�ѩ�
b 0, �G b + c
0, �G b + c c.
c.
�� a ���O zero-divisor ��, �W���һ������n���p�N���|�o��.
Lemma 5.3.3
��
a  R
R ���O ring
R ���� zero-divisor ��, �Y
a . b =
a . c ��
b . a =
c . a, �h
b =
c.
�� ��.
���p
a . b =
a . c, �Y
a . b -
a . c = 0. �� Lemma
5.2.3 ��
- (
a . c) =
a . (-
c) �G
0 = a . b - a . c = a . b + a . (- c) = a . (b - c).
�M��
a ���O zero-divisor,
�]���Y
b -
c
0, �h
a . (
b -
c)

0. �G�Ѧ���
b -
c = 0, �]�N�O��
b =
c. �P�z�i�ҭY
b . a =
c . a, �h
b =
c.

�`��, ���A�b�B�z ring �����D�ɵo� a 0 �B
a . b = a . c
�A���i�H���W�U���� b = c, ���D�A���D�o�� ring ���S�� zero-divisor.
�ҥH�@�ӨS�� zero-divisor �� ring �ȱo�S�O�����@�ӦW�l.
0 �B
a . b = a . c
�A���i�H���W�U���� b = c, ���D�A���D�o�� ring ���S�� zero-divisor.
�ҥH�@�ӨS�� zero-divisor �� ring �ȱo�S�O�����@�ӦW�l.
Definition 5.3.4
�p�G R �O�@�� ring �B R ���S�� zero-divisor, �h�� R �O�@��
domain. �p�G R �O�@�� commutative ring with 1 �B�O�@��
domain, �h�٤����@�� integral domain.
���
 �ҧΦ��� ring �N�O�̨嫬�� integral domain.
�ҧΦ��� ring �N�O�̨嫬�� integral domain.
�Y R �O�@�� ring with 1, �h R �����i��s�b�����������k inverse
�]�b R ��. �o�˪������]���ܯS�O���ʽ�.
Definition 5.3.5
�Y
R �O�@�� ring with 1, �p�G
a  R
R �B�s�b
b  R
R �ϱo
a . b =
b . a = 1, �h��
a �O
R ���@��
unit.
���M�F�b�w�q�̪� b �]�O R �� unit. �Q�� Proposition 1.2.2
�@�˪��ҩ��ڭ̥i�H�o��o�� b �b R ���O�ߤ@��. �ҥH�� a �O�@��
unit �ɧڭ̳q�`�|�� a-1 ���ܨ䭼�k�� inverse.
Example 5.3.6
�b

/6

�o�� ring ��
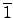
�O

/6

�� 1 (���k��
identity). �]
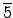 .
. 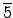
=
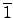
, �G
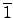
�M
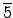
�O
unit. ��L������

,
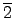
,
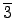
,
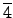
�����O unit.
Unit ���H�U�ܦn���ʽ�:
Lemma 5.3.7
�Y
R �O�@�� ring with 1 �B
a  R
R �O�@�� unit, �h
- a ���藍�|�O 0, �]���|�O R �����@�� zero-divisor.
- ����N�� b
 R, �赦�
a . x = b �M
y . a = b �b R
�����|���ߤ@����.
R, �赦�
a . x = b �M
y . a = b �b R
�����|���ߤ@����.
�� ��.
(1) �Y
a = 0, �h�� Lemma
5.2.1 ��
a ���W
R
�������������� 0, �G���i����@����
b �ϱo
a . b = 1.
���M
a �O unit �٬�, �ҥH
a
0.
�p�G a �O�@�� zero divisor, ���ܦs�b c 0 �ϱo
a . c = 0 ��
c . a = 0. ���]�O
a . c = 0, �Ѱ��] a �O unit ��
a-1
0 �ϱo
a . c = 0 ��
c . a = 0. ���]�O
a . c = 0, �Ѱ��] a �O unit ��
a-1  R, �G�o
R, �G�o
0 = a-1 . (a . c) = c.
���M
c
0 �٬�, �G��
a
���O zero-divisor. �P�z�i��
c . a = 0 �����p.
(2) ����N b  R, �Ѱ��] a �O unit ��
a-1
R, �Ѱ��] a �O unit ��
a-1  R, �G�O
x = a-1 . b
R, �G�O
x = a-1 . b  R �i�o
R �i�o
a . x = a . (a-1 . b) = b.
�Y
x'  R
R �]����
a . x' =
b, �]�N�O��
a . x =
a . x', �h��
(1) ��
a ���O zero-divisor �A�[�W Lemma
5.3.3 ��
x =
x'.
�]���i��
a . x =
b �b
R ���s�b�ߤ@����. �P�z
y . a =
b �b
R ���]���ߤ@����.

�ڭ̱j�դ@�U, �@�� ring ���� unit ���藍�O zero-divisor,
���L�Y�@�Ӥ������O zero-divisor �ä����ܥ��|�O unit. �Ҧp�b
 ��
2 ���O zero-divisor, �����]���O
��
2 ���O zero-divisor, �����]���O
 �� unit.
�� unit.
�� Lemma 5.3.7 ���b R �� 0 ���藍�|�O�@�� unit. �p�G���F
0 �H� ��L���������O unit �o��S�O�� ring
�]�ȱo�����@�ӯS�O���W�l.
Definition 5.3.8
�Y R �O�@�� ring with 1 �B R ���D 0 ���������O unit, �h��
R �O�@�� division ring. �Y R �O�@�� commutative ring
�B�O�@�� division ring, �h�� R �O�@�� field.
���z��
 �Ҧ��� ring �N�O�@�Ө嫬�� field.
�Ҧ��� ring �N�O�@�Ө嫬�� field.
�̫�ڭ̭n�j��: �p�G R �O�@�� division ring, �h�ѩ� R �����D 0
�������O unit �ҥH�����O zero-divisor. �]����ӫD 0
�����ۭ��������� 0. �]�N�O R ���D 0
�������Ҧ������X�b���k���U�O�ʳ���. �A�[�W�o�Ǥ����������k��
inverse, �ҥH R ���D 0 �������Ҧ������X�b���k���U�O�@�� group.
�ר�� R �O�@�� field ��, R ���D 0
�������Ҧ������X�b���k���U�O�@�� abelian group.



�U�@��: Subring
�W�@��: ��� Ring ���ʽ�
�e�@��: �� Ring ���w�q�ұo���ʽ�
Administrator
2005-06-18
![]() y (�άO
x . a = y . a ���O x
y (�άO
x . a = y . a ���O x![]() y).
�Ҧp�b
y).
�Ҧp�b
![]() /6
/6![]() ���ڭ̤����o�
���ڭ̤����o�
![]() .
. ![]() =
= ![]() .
. ![]() =
= ![]() . �|�ɭP�o�˪��O�o�ͬO�]���Y a �O
zero-divisor, ���] b
. �|�ɭP�o�˪��O�o�ͬO�]���Y a �O
zero-divisor, ���] b![]() 0 ����
a . b = 0 (��
b . a = 0). �h
0 ����
a . b = 0 (��
b . a = 0). �h
![]() 0 �B
a . b = a . c
�A���i�H���W�U���� b = c, ���D�A���D�o�� ring ���S�� zero-divisor.
�ҥH�@�ӨS�� zero-divisor �� ring �ȱo�S�O�����@�ӦW�l.
0 �B
a . b = a . c
�A���i�H���W�U���� b = c, ���D�A���D�o�� ring ���S�� zero-divisor.
�ҥH�@�ӨS�� zero-divisor �� ring �ȱo�S�O�����@�ӦW�l.
![]() �ҧΦ��� ring �N�O�̨嫬�� integral domain.
�ҧΦ��� ring �N�O�̨嫬�� integral domain.
![]() 0 �ϱo
a . c = 0 ��
c . a = 0. ���]�O
a . c = 0, �Ѱ��] a �O unit ��
a-1
0 �ϱo
a . c = 0 ��
c . a = 0. ���]�O
a . c = 0, �Ѱ��] a �O unit ��
a-1 ![]() R, �G�o
R, �G�o
![]() R, �Ѱ��] a �O unit ��
a-1
R, �Ѱ��] a �O unit ��
a-1 ![]() R, �G�O
x = a-1 . b
R, �G�O
x = a-1 . b ![]() R �i�o
R �i�o
![]() ��
2 ���O zero-divisor, �����]���O
��
2 ���O zero-divisor, �����]���O
![]() �� unit.
�� unit.
![]() �Ҧ��� ring �N�O�@�Ө嫬�� field.
�Ҧ��� ring �N�O�@�Ө嫬�� field.