next up previous
下一頁: 一些 Noncommutative Ring 上一頁: 初級 Ring 的性質 前一頁: Zero Divisor 和 Unit

Subring

在研究 group 時我們曾經探討過 subgroup. 同樣的對於一個 ring 我們也探討它的 subring.

首先我們給 subring 一個正式的定義.

Definition 5.4.1   若 R 是一個 ring, S $ \subseteq$ R 且利用 R 的加法與乘法為其運算 S 也是一個 ring, 則稱 S 是 R 的一個 subring.

雖然 S 必須符合 (R1) 到 (R8) 的性質 S � 可成為 R 的一個 subring, 不過和 subgroup 的情況一樣結合率因在 R 中已經符合了所以 (R2) 和 (R7) 是不必檢查的. 另� 加法的交換性 (R5) 和分配率 (R8) 也在 R 中已符合了所以我們只要檢查 (R1), (R3), (R4) 和 (R5). 也就是說我們只要檢查 S 在加法之下是否為 R 加法之下的 subgroup 以及 S 在乘法之下是否封閉就可以了. 因此我們有以下之結果.

Lemma 5.4.2   若 R 是一個 ring, S $ \subseteq$ R. 如果對於任意的 a, b $ \in$ S 皆有 a - b $ \in$ S 且 a . b $ \in$ S, 則 S 是 R 的 subring.

証 明. 由 Lemma 1.3.4 知, 若對任意 a, b $ \in$ S 皆有 a - b $ \in$ S, 表示 S 在加法之下是 R 的 subgroup. 再加上 a . b $ \in$ S 表示乘法是封閉的, 所以 S 是 R 的一個 subring. $ \qedsymbol$

Example 5.4.3   讓我們考� $ \mathbb {Z}$/6$ \mathbb {Z}$ 有哪些 subring? 由於 subring 在加法之下一定是 subgroup. 所以我們只要先把 $ \mathbb {Z}$/6$ \mathbb {Z}$ 加法的 subgroup 都找出來, 再看看他們是否乘法封閉就可以了. 因 $ \mathbb {Z}$/6$ \mathbb {Z}$ 在加法之下是一個 order 6 = 2×3 的 abelian group, 由 Lagrange 和 Cauchy 定理 (Theorem 2.2.2 & Theorem 3.3.2) 知其有 order 3 和 order 2 的 subgroups (事實上這可以由 $ \mathbb {Z}$/6$ \mathbb {Z}$ 在加法之下是一個 cyclic group 直接看出). 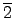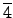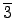也就是 {$ \overline{0}$,$ \overline{2}$,$ \overline{4}$} 和 {$ \overline{0}$,$ \overline{3}$} 這兩個 subgroups. 很容易就可以知道這兩個子集合都是乘法封閉的, 所以它們也都是 $ \mathbb {Z}$/6$ \mathbb {Z}$ 的 subrings.

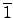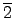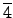在討論 subgroup 時我們提過: 若 G 是一個 group, H 為其 subgroup, 則 H 的 identity 就是 G 的 identity. 所以當 R 是一個 ring 時, 若 S 為其 subring, 則 S 的 0 就是 R 的 0. 不過因 R 和 S 的乘法不一定是 group, 即使 R 有乘法的 identity 1, S 未必會有 1. 縱使 S 有 1, S 的 1 和 R 的 1 也未必相同. 例如前面 Example 5.4.3 中 $ \mathbb {Z}$/6$ \mathbb {Z}$ 的 1 是 $ \overline{1}$. 而在 {$ \overline{0}$,$ \overline{2}$,$ \overline{4}$} 這個 subring 中

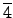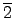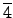$\displaystyle \overline{0}$ . $\displaystyle \overline{4}$ = $\displaystyle \overline{0}$,    $\displaystyle \overline{2}$ . $\displaystyle \overline{4}$ = $\displaystyle \overline{2}$,    $\displaystyle \overline{4}$ . $\displaystyle \overline{4}$ = $\displaystyle \overline{4}$,

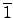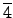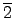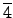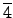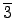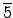所以 $ \overline{4}$ 是 {$ \overline{0}$,$ \overline{2}$,$ \overline{4}$} 這個 subring 的 1. 注意這並沒有和前面提過一個 ring 若有乘法的 identity 則其 identity 唯一相違背. $ \overline{1}$ 是 $ \mathbb {Z}$/6$ \mathbb {Z}$ 中唯一的 1, 而 $ \overline{4}$ 是 {$ \overline{0}$,$ \overline{2}$,$ \overline{4}$} 中唯一的 1. 只是 $ \overline{4}$ 在 $ \mathbb {Z}$/6$ \mathbb {Z}$ 中它不再是 1 膜F! (它碰到 $ \overline{3}$ 和 $ \overline{5}$ 就沒輒了.)

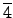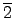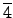另� 大家應也發� $ \overline{4}$ 在 $ \mathbb {Z}$/6$ \mathbb {Z}$ 是一個 zero-divisor, 但在 {$ \overline{0}$,$ \overline{2}$,$ \overline{4}$} 中卻是一個 unit. 這當然也沒和 Lemma 5.3.7 (1) 相衝突, 因為這是在不同的 ring 之下. 總之, 一個 ring 中的元素很可能在 ring 中和在 subring 中會有截然不同的表�.

next up previous
下一頁: 一些 Noncommutative Ring 上一頁: 初級 Ring 的性質 前一頁: Zero Divisor 和 Unit
Administrator 2005-06-18