


下一頁: 一些 abelian groups 特有的性質
上一頁: Finite Abelian Groups
前一頁: Finite Abelian Groups
G 是 abelian 最好的地方是 G 的任意的 subgroup 都是 normal.
所以很多有關 abelian groups 的性質我們都可以在 G 中找到一個
subgroup 然後再做 quotient group 這樣新的 group 的 order 變小了,
我們就可以用數學歸納法.
要用這種取 quotient group 的數學歸納法一般來說會牽扯上
Correspondence 定理 (忘記這是什麼的同學趕快退回去看一下 Corollary
2.7.3), 另外就是考慮
ord(a) 和
ord( ) 的關係了.
下一個 Lemma 就是告訴我們這個關係, 要注意的是這個 Lemma 並不需要
abelian 的假設:
) 的關係了.
下一個 Lemma 就是告訴我們這個關係, 要注意的是這個 Lemma 並不需要
abelian 的假設:
Lemma 3.3.1
若
N 是 group
G 的一個 normal subgroup,
a  G
G. 考慮

 G
G/
N, 則
ord(
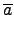
) | ord(
a).
而且
ord(

) = ord(
a) 若且為若
証 明.
假設
ord(
a) =
n. 則因
an =
e 得
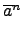
=
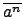
=
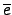
, 故由
Lemma
2.3.2 知
ord (

) |
n.
假設
ord( ) = m. 今若
N
) = m. 今若
N 
 a
a = {e}, 則因
= {e}, 則因
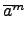 =
= 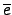 表示 am
表示 am  N, 所以得
am
N, 所以得
am  N
N 
 a
a = {e}. 換句話說 am = e, 再由 Lemma 2.3.2 得
ord(a) = n | m. 然而前已知 m | n, 所以 n = m: 也就是說如果
N
= {e}. 換句話說 am = e, 再由 Lemma 2.3.2 得
ord(a) = n | m. 然而前已知 m | n, 所以 n = m: 也就是說如果
N 
 a
a = {e}, 則
ord(
= {e}, 則
ord( ) = ord(a).
) = ord(a).
反之, 假設
ord( ) = ord(a). 若
x
) = ord(a). 若
x  N
N 
 a
a ,
由
x
,
由
x 
 a
a 知: 存在一整數 i 使得 x = ai. 不過又由
x
知: 存在一整數 i 使得 x = ai. 不過又由
x  N, 知
N, 知
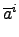 =
= 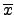 =
= 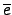 . 由此知
ord(
. 由此知
ord( ) | i.
然而由假設
ord(
) | i.
然而由假設
ord( ) = ord(a) 得
ord(a) | i, 因此得證
x = ai = e. 也就是說若
ord(
) = ord(a) 得
ord(a) | i, 因此得證
x = ai = e. 也就是說若
ord( ) = ord(a) 則
N
) = ord(a) 則
N 
 a
a = {e}.
= {e}. 
以下就是利用數學歸納法來證明一些 abelian groups 的性質的例子:
Theorem 3.3.2 (Cauchy's Theorem for Abelian Groups)
若
G 是一個 finite abelian group,
p 是一個質數, 且
p 整除
G
的 order, 則
G 中存在一個元素其 order 為
p.
証 明.
前面提過我們要用 induction 來證明此定理. 如何用 induction 呢?
我們將對所有的 finite abelian group 的 order 作 induction.
也就是我們將證明這個定理對 order 為
p 的 abelian group 是對的.
然後利用歸納法假設對 order 小於
pk 的 abelian group 也對,
來證出對於 order 為
pk 的 abelian group 也對.
假設 G 的 order 為 p, 由 Corollary 2.2.3 知 G 是一個
cyclic group, 所以若 a  G 使得
G =
G 使得
G =  a
a , 則
ord(a) = p.
, 則
ord(a) = p.
現在假設對於所有的 abelian group G' 如果 | G'| = pr 且 r < k,
則存在 a  G' 使得
ord(a) = p. 若 | G| = pk, 則有以下三種狀況:
G' 使得
ord(a) = p. 若 | G| = pk, 則有以下三種狀況:
- G 中無 nontrivial proper subgroup.
- G 中有一 nontrivial proper subgroup H 且 p 整除 | H|.
- G 中所有的 nontrivial proper subgroup 其 order 都不能被 p 整除.
如果是狀況 1. 則由 Lemma
3.1.2 知 |
G| =
p, 這情形已證過.
如果是狀況 2. 則因
H 是 nontrivial proper subgroup 故 |
H| < |
G|,
而
p 整除 |
H| 故 |
H| =
pr, 其中
r <
k. 故由 induction
的假設之存在
a  H
H 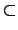 G
G 且
ord(
a) =
p. 所以在這情況也得證.
我們真正得處理的就是狀況 3. 在這情況之下我們任取一個
G 的
nontrivial proper subgroup
H, 然後考慮
G/
H 這個 quotient group
(別忘了在此我們用到
G 是 abelian 故
H 是 normal). 由於
p
|
H|, 所以
p 整除
|
G/
H| = |
G|/|
H|. 再加上
G/
H 仍是
abelian group 且 |
G/
H| < |
G| 所以我們可以套用 induction 的假設在
G/
H 上, 也就是存在

 G
G/
H 且
ord(

) =
p. 現在我們利用前面的 Lemma
3.3.1 知
p | ord(
a); 也就是存在正整數
t 使得
ord(
a) =
pt. 利用
Proposition
2.3.3 得
ord(
at) =
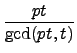
=
p.
得證在
G 中存在一元素
at 其 order 為
p.

這裡要強調這裡我們證的 Cauchy's Theorem 是利用 G 是 abelian
的假設下證明, 雖然這一個證明對 G 不是 abelian 時並不適用,
不過將來我們會用另外的方法證明一般的 Cauchy's Theorem.
也就是說這個定理在 G 不是 abelian 時仍是對的.
我們可以用類似的方法證以下的定理:
Theorem 3.3.3 (Sylow's Theorem for Abelian Groups)
若
G 是一個 finite abelian group, 且 |
G| =
pnm, 其中
p 是
質數且
p m
m, 則在
G 中存在一個 subgroup
P 其 order 為
pn.
証 明.
我們用類似前面 Theorem
3.3.2 的 induction. 當 |
G| =
pm 時,
Theorem
3.3.2 告訴我們存在
a  G
G 其 order 為
p, 故此時取
P =
 a
a
即可.
現在假設當 | G'| = prm, r < n 時, 在 G' 中可找到 subgroup P' 其
order 為 pr. 當 | G| = pnm 時, 由 Theorem 3.3.2 知存在 G
的 subgroup N 其 order 為 p. 因 G 是 abelian 故 N 是 G 的
normal subgroup, 故考慮 G/N 這一個 quotient group. G/N 的 order
是
| G|/| N| = pn - 1m. 故由 induction 的假設知在 G/N 中存在一個
subgroup P' 其 order 為 pn - 1. 再利用 Correspondence 定理
(Corollary 2.7.3) 知 G 中存在一 subgroup P 使得 P' = P/N.
然而
| P| = | P'| . | N| = pn - 1 . p = pn, 故得證.

若 p 是一個質數, 而一個 group 的個數是 pn 這種形式時,
我們稱這種 group 為一個 p-group. 當 G 的個數是 pnm,
其中 p 和 m 互質時, 若 G 中的 subgroup H 其 order 又剛好是
pn, 則稱 H 是 G 的一個 Sylow p-subgroup. Theorem
3.3.3 告訴我們當 G 是一個 abelian group 時, 其 Sylow
p-subgroup 一定存在. 以後我們也會學到在一般的 group 中 Sylow
p-subgroup 也一定存在, 這就是所謂的 Sylow 定理.



下一頁: 一些 abelian groups 特有的性質
上一頁: Finite Abelian Groups
前一頁: Finite Abelian Groups
Administrator
2005-06-18
![]() ) 的關係了.
下一個 Lemma 就是告訴我們這個關係, 要注意的是這個 Lemma 並不需要
abelian 的假設:
) 的關係了.
下一個 Lemma 就是告訴我們這個關係, 要注意的是這個 Lemma 並不需要
abelian 的假設:
![]() ) = m. 今若
N
) = m. 今若
N ![]()
![]() a
a![]() = {e}, 則因
= {e}, 則因
![]() =
= ![]() 表示 am
表示 am ![]() N, 所以得
am
N, 所以得
am ![]() N
N ![]()
![]() a
a![]() = {e}. 換句話說 am = e, 再由 Lemma 2.3.2 得
ord(a) = n | m. 然而前已知 m | n, 所以 n = m: 也就是說如果
N
= {e}. 換句話說 am = e, 再由 Lemma 2.3.2 得
ord(a) = n | m. 然而前已知 m | n, 所以 n = m: 也就是說如果
N ![]()
![]() a
a![]() = {e}, 則
ord(
= {e}, 則
ord(![]() ) = ord(a).
) = ord(a).
![]() ) = ord(a). 若
x
) = ord(a). 若
x ![]() N
N ![]()
![]() a
a![]() ,
由
x
,
由
x ![]()
![]() a
a![]() 知: 存在一整數 i 使得 x = ai. 不過又由
x
知: 存在一整數 i 使得 x = ai. 不過又由
x ![]() N, 知
N, 知
![]() =
= ![]() =
= ![]() . 由此知
ord(
. 由此知
ord(![]() ) | i.
然而由假設
ord(
) | i.
然而由假設
ord(![]() ) = ord(a) 得
ord(a) | i, 因此得證
x = ai = e. 也就是說若
ord(
) = ord(a) 得
ord(a) | i, 因此得證
x = ai = e. 也就是說若
ord(![]() ) = ord(a) 則
N
) = ord(a) 則
N ![]()
![]() a
a![]() = {e}.
= {e}. ![]()
![]() G 使得
G =
G 使得
G = ![]() a
a![]() , 則
ord(a) = p.
, 則
ord(a) = p.
![]() G' 使得
ord(a) = p. 若 | G| = pk, 則有以下三種狀況:
G' 使得
ord(a) = p. 若 | G| = pk, 則有以下三種狀況:
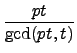 = p.
= p.
![]()