

下一頁: Normal Subgroups 和 Quotient
上一頁: 中級 Group 的性質
前一頁: Lagrange's Theorem
前面定義過一個 group 的 order 為其元素的個數. 而一個 group 中的元素
a, 其產生的 cyclic group
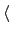 a
a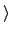 的 order 就稱為此元素
a 的 order. 我們記為
ord(a). 若 G 為一個 group 且 a
的 order 就稱為此元素
a 的 order. 我們記為
ord(a). 若 G 為一個 group 且 a  G,
由 Lagrange's Theorem 知
ord(a) | | G|. 因此若我們知 G
中元素的 order 或多或少就可知道 G 的 order 的一些訊息, 反之亦然.
G,
由 Lagrange's Theorem 知
ord(a) | | G|. 因此若我們知 G
中元素的 order 或多或少就可知道 G 的 order 的一些訊息, 反之亦然.
以下的 Lemma 給我們一個明確的方法來計算一個元素的 order.
Lemma 2.3.1
令
a 為一個 group
G 中的元素,
e 為
G 的 identity. 假設
n 
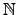
是最小的正整數使得
an =
e, 則
ord(
a) =
n.
証 明.
我們要證明當
n 是最小的正整數使得
an =
e 則
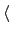 a
a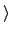
有
n 個元素. 事實上我們要證明
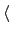 a
a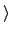
= {
e,
a,
a2,...,
an - 1}. 首先回顧
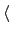 a
a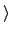
中的元素都是
ak,
k 

這種形式. 利用整數的餘數定理: 當
n > 1
時, 可以找到整數
h 和
r 使得
k =
h . n +
r, 其中 0
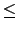 r
r <
n.
因此
ak = ah . n + r = (an)h . ar = e . ar = ar.
換句話說我們利用
an =
e 得到
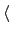 a
a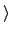
中的元素可表為
ar, 0
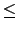 r
r <
n 這種形式, 也就是說
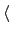 a
a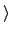
= {
e,
a,
a2,...,
an - 1}. 但這並不表示
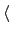 a
a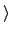
有
n
個元素, 除非我們知道它們都相異. 因此我們還得證明當
0
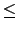 i
i <
j <
n 時,
ai aj
aj. 別忘了我們尚未用到
n 是最小的這個性質. 如果
0
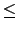 i
i <
j <
n 且
ai =
aj, 則
aj - i =
aj . a-i =
e. 但
j -
i 
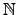
且
n >
j -
i. 這和
n 是最小的正整數使得
an =
e 矛盾. 故
aj ai
ai. 也就是說
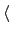 a
a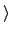
的 order 為
n.

假設 a 的 order 為 n. 由 n 是最小的正整數使得 an = e
這個性質知如果
m 
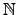 且 am = e, 則 m
且 am = e, 則 m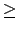 n. 事實上我們可得到
m 與 n 更好的關係式.
n. 事實上我們可得到
m 與 n 更好的關係式.
Lemma 2.3.2
令
a 為 group
G 中的一元素. 若
am =
e, 則
ord(
a) |
m.
証 明.
假設
ord(
a) =
n. 利用整數的餘數定理, 存在整數
h 及
r, 其中
0
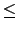 r
r <
n 使得
m =
n . h +
r. 故得
am = an . h . ar = e . ar = ar.
也就是說
ar =
e. 如果
r
0, 則
r
是一個比
n 還小的正整數使得
ar =
e. 此和 Lemma
2.3.1
相違背. 故知
r = 0; 換句話說
n 可整除
m.

當然了, 從若 am = e 則 n | m 這個性質我們可推得 n
是最小的正整數滿足 an = e. 所以整合 Lemma 2.3.1 及 Lemma
2.3.2, 當我們要說
ord(a) = n 時, 我們只要驗證:
- an = e.
- 若 am = e 則 n | m.
下一個 Proposition 不但是一個很有用的定理,
而且其證明可以幫助我們了解前面提到如何驗證一個元素的 order 的方法.
証 明.
為了方便, 我們令
d = gcd(
i,
n). 欲證明
ord(
ai) =
n/
d, 首先得證明
(
ai)
n/d =
e. 事實上因為
d 是
i 的因數,
i/
d 是個整數.
再加上由假設
n 為
a 的 order, 故
an =
e. 所以可得
(
ai)
n/d = (
an)
i/d =
e.
接下來我們須證明, 若 (ai)m = e 則
(n/d ) | m. 若 (ai)m = e,
即 ami = e. 故由 Lemma 2.3.2, 我們可得 n | mi. 但因 d
是 n 和 i 的最大公因數. 我們有 n/d 和 i/d 皆為整數且互質.
故由 n | mi 可得
(n/d ) | m(i/d ). 再由 n/d 和 i/d 互質,
得
(n/d ) | m.

讓我們回到 Lagrange's Theorem 的應用. 若 G 是一個 finite group, 而
a  G, 則 Lagrange's Theorem (2.2.2) 告訴我們說:
G, 則 Lagrange's Theorem (2.2.2) 告訴我們說:
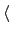 a
a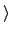 的 order 整除 G 的 order. 也就是說若 a 的 order 為
m, G 的 order 為 n, 則存在
r
的 order 整除 G 的 order. 也就是說若 a 的 order 為
m, G 的 order 為 n, 則存在
r 
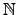 使得
n = m . r. 又因
a 的 order 為 m, 由 Lemma 2.3.1 知 am = e. 故
an = amr = (am)r = e. 因此我們有以下重要的結果.
使得
n = m . r. 又因
a 的 order 為 m, 由 Lemma 2.3.1 知 am = e. 故
an = amr = (am)r = e. 因此我們有以下重要的結果.
Corollary 2.3.4
若
G 是一個 finite group, 且其 order 為
n. 令
a  G
G 是
G
中一元素. 則
an =
e.


下一頁: Normal Subgroups 和 Quotient
上一頁: 中級 Group 的性質
前一頁: Lagrange's Theorem
Administrator
2005-06-18
![]()
![]() 且 am = e, 則 m
且 am = e, 則 m![]() n. 事實上我們可得到
m 與 n 更好的關係式.
n. 事實上我們可得到
m 與 n 更好的關係式.
![]()
![]() G, 則 Lagrange's Theorem (2.2.2) 告訴我們說:
G, 則 Lagrange's Theorem (2.2.2) 告訴我們說:
![]() a
a![]() 的 order 整除 G 的 order. 也就是說若 a 的 order 為
m, G 的 order 為 n, 則存在
r
的 order 整除 G 的 order. 也就是說若 a 的 order 為
m, G 的 order 為 n, 則存在
r ![]()
![]() 使得
n = m . r. 又因
a 的 order 為 m, 由 Lemma 2.3.1 知 am = e. 故
an = amr = (am)r = e. 因此我們有以下重要的結果.
使得
n = m . r. 又因
a 的 order 為 m, 由 Lemma 2.3.1 知 am = e. 故
an = amr = (am)r = e. 因此我們有以下重要的結果.