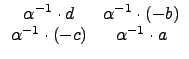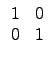¤U¤@¶: The Hamilton quaternions
¤W¤@¶: ¤@¨Ç Noncommutative Ring
«e¤@¶: ¤@¨Ç Noncommutative Ring
ĄO R ¬O¤@Ó commutative ring with
1. ¦ŇĽ¶°¦X M2(R) ¬O©Ň¦ł«YĽĆ¦b R Şş 2×2
Żx°©Ň¦¨Şş¶°¦X, ¤]´N¬O»ˇ M2(R) ¤¤Şş¤¸ŻŔłŁ¬O
łoşŘ§Î¦ˇ¨ä¤¤
a, b, c, d  R. ¦]¬° R ¬O¤@Ó ring
§ÚĚĄiĄH©w M2(R) ¤¤ŞşĄ[Şk©MĽŞk´N¬O¤@ŻëŻx°ŞşĄ[Şk©MĽŞk, §Y:
¦]¬° R ¬O¤@Ó ring with 1,
¤ŁĂřµo˛ĄH¤WŞşĄ[Şk©MĽŞk¨Ď±o
M2(R) ¦¨¬°¤@Ó ring, ¦ÓĄB
R. ¦]¬° R ¬O¤@Ó ring
§ÚĚĄiĄH©w M2(R) ¤¤ŞşĄ[Şk©MĽŞk´N¬O¤@ŻëŻx°ŞşĄ[Şk©MĽŞk, §Y:
¦]¬° R ¬O¤@Ó ring with 1,
¤ŁĂřµo˛ĄH¤WŞşĄ[Şk©MĽŞk¨Ď±o
M2(R) ¦¨¬°¤@Ó ring, ¦ÓĄB

 ©M
©M
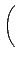
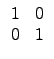
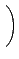 ¤Ŕ§O¬O M2(R) Şş 0 ©M 1. ©ŇĄH»ˇ M2(R) ¬O¤@Ó ring
with 1. ¤ŁąL§Y¨Ď R ¬O commutative, M2(R) ¤]¤Ł·|¬O commutative
ring. łoĄiĄŃĄH¤UŞş¨Ň¤l¬ÝĄX:
(Ş`·N: ·í§ÚĚn»ˇ©ú¤@Ó ring R ¬O commutative ®É,
§ÚĚĄ˛¶·ĂŇ©úąďĄô·NŞş a, b
¤Ŕ§O¬O M2(R) Şş 0 ©M 1. ©ŇĄH»ˇ M2(R) ¬O¤@Ó ring
with 1. ¤ŁąL§Y¨Ď R ¬O commutative, M2(R) ¤]¤Ł·|¬O commutative
ring. łoĄiĄŃĄH¤UŞş¨Ň¤l¬ÝĄX:
(Ş`·N: ·í§ÚĚn»ˇ©ú¤@Ó ring R ¬O commutative ®É,
§ÚĚĄ˛¶·ĂŇ©úąďĄô·NŞş a, b  R ¬Ň¦ł
a . b = b . a.
¤ŁąLYn»ˇ©ú R ¬O noncommutative ®É, Ąun§ä¨ě¤@˛Ő a, b
R ¬Ň¦ł
a . b = b . a.
¤ŁąLYn»ˇ©ú R ¬O noncommutative ®É, Ąun§ä¨ě¤@˛Ő a, b  R ¨Ď±o
a . b
R ¨Ď±o
a . b b . a §YĄi.)
b . a §YĄi.)
±q¤W±Şş¦ˇ¤l§ÚĚŞľąD
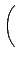
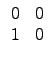
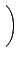 ©M
©M
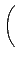
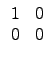
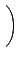 ¬O M2(R) Şş zero-divisor.
¦P®É¦błoӨҤl¸Ě§Ṳ́]µo˛¦b¤@Ó noncommutative ring ¤¤¬O¦łĄiŻŕµoĄÍ
a . b = 0 ¦ý
b . a
¬O M2(R) Şş zero-divisor.
¦P®É¦błoӨҤl¸Ě§Ṳ́]µo˛¦b¤@Ó noncommutative ring ¤¤¬O¦łĄiŻŕµoĄÍ
a . b = 0 ¦ý
b . a 0 Şş˛¶H.
0 Şş˛¶H.
±µ¤U¨Ó§ÚĚ·Q§ä¨ě M2(R) ¤¤©Ň¦łŞş zero-divisor ©M unit.
şĄýĆ[ąîĄH¤UŞş¦ˇ¤l:
nŞ`·N§ÚĚ»Ýn R ¬O commutative ¦ˇ¤l (5.2) ¤ ·|ąď.
¤j®aŔł¸Óąď
a . d - b . c łoÓȤŁŻĄÍ, Ą¦¬O
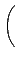
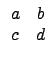
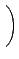 Şş determinant. łq±`µą¤@Żx°
A
Şş determinant. łq±`µą¤@Żx°
A  M2(R) §ÚĚĄÎ
det(A) ŞíĄÜ¨ä determinant. ĄŃ©ó R ¬O¤@Ó ring, ©ŇĄHąďĄô·NŞş
A
M2(R) §ÚĚĄÎ
det(A) ŞíĄÜ¨ä determinant. ĄŃ©ó R ¬O¤@Ó ring, ©ŇĄHąďĄô·NŞş
A  M2(R), §ÚĚłŁĄi±o
det(A)
M2(R), §ÚĚłŁĄi±o
det(A)  R. Determinant
Á٦łĄH¤UłoÓ«nŞş©Ę˝č:
R. Determinant
Á٦łĄH¤UłoÓ«nŞş©Ę˝č:
det(A . B) = det(A) . det(B), 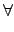 A, B A, B  M2(R). M2(R). |
(5.3) |
¨ě©ł M2(R) ¤¤¦łţ¨Ç zero-divisor ©O? ¦PľÇĄiŻŕ·Q¨ě determinant ¬° 0 Şş¤¸ŻŔ. ¨Sżů, ·í
A = 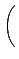
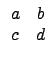
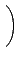

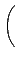

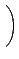 ¦ý det(A) = 0 ®É, ĄŃ©ó
¦ý det(A) = 0 ®É, ĄŃ©ó
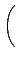
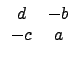
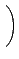

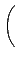

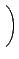 , ĄŃ¦ˇ¤l (5.2) Şľ A ¬O¤@Ó zero-divisor.
, ĄŃ¦ˇ¤l (5.2) Şľ A ¬O¤@Ó zero-divisor.
Á٦ł¨S¦ł¨äĄLŞş zero-divisor ©O? ¨äąę·í det(A) ¬O R Şş
zero-divisor ®É,
A ¤]·|¬O M2(R) Şş zero-divisor. ło¬O¦]¬°¦pŞG
A = 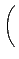
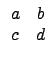
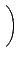

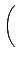

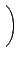 ĄB
det(A) =
ĄB
det(A) =  ¬O R Şş¤@Ó zero-divisor. ł]
¬O R Şş¤@Ó zero-divisor. ł]
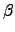
 0 ¬O R ¤¤¤@¤¸ŻŔşˇ¨¬
0 ¬O R ¤¤¤@¤¸ŻŔşˇ¨¬
 .
. 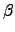 = 0.
¦łĄH¤U¨âşŘĄiŻŕµoĄÍ:
= 0.
¦łĄH¤U¨âşŘĄiŻŕµoĄÍ:
(1)
a . 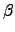 ,
b .
,
b . 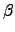 ,
c .
,
c . 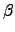 ©M
d .
©M
d . 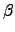 łŁµĄ©ó 0: ¦ą®ÉĄO
B =
łŁµĄ©ó 0: ¦ą®ÉĄO
B = 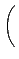
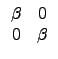
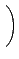 , ¦p¦ą¤@¨Ó¦]
, ¦p¦ą¤@¨Ó¦]
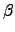
 0, ©ŇĄH
B
0, ©ŇĄH
B
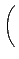

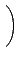 , ¦ý¬O
, ¦ý¬O
¦]¦ą¦błoÓ±ˇ§Î®É, A ¬O M2(R) Şş¤@Ó zero-divisor.
(2)
a . 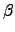 ,
b .
,
b . 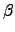 ,
c .
,
c . 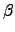 ©M
d .
©M
d . 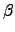 ¤ŁĄţ¬° 0:
«h§Ú̦Ҽ
¤ŁĄţ¬° 0:
«h§Ú̦Ҽ
µM¦Ó
ĄŃ¦ˇ¤l (5.2) Şľ
©ŇĄH¦błoÓ±ˇŞp A Á٬O M2(R) Şş¤@Ó zero-divisor.
¨ş»ň·í
A = 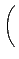
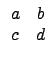
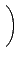 ĄB
det(A) =
ĄB
det(A) =  ¤Ł¬O R Şş zero-divisor ®É¤S·|«çĽË©O? °˛ł]¦s¦b
B =
¤Ł¬O R Şş zero-divisor ®É¤S·|«çĽË©O? °˛ł]¦s¦b
B = 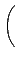
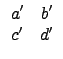
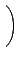


 (¤]´N¬O»ˇ a', b', c' ©M d' ¤ŁĄţ¬° 0) şˇ¨¬
A . B =
(¤]´N¬O»ˇ a', b', c' ©M d' ¤ŁĄţ¬° 0) şˇ¨¬
A . B = 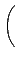

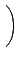 . ¦ą®É¦ŇĽ
C =
. ¦ą®É¦ŇĽ
C = 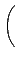
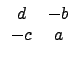
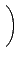 , «hĄŃ¦ˇ¤l (5.2) Şľ
, «hĄŃ¦ˇ¤l (5.2) Şľ
¦]¬°  ¤Ł¬O zero-divisor ĄB a', b', c' ©M
d' ¤ŁĄţ¬° 0, ©ŇĄHŞľ
¤Ł¬O zero-divisor ĄB a', b', c' ©M
d' ¤ŁĄţ¬° 0, ©ŇĄHŞľ
 . a',
. a',
 . b',
. b',
 . c' ©M
. c' ©M
 . d' ¤ŁĄţ¬° 0. ¤]´N¬O»ˇ
(C . A) . B
. d' ¤ŁĄţ¬° 0. ¤]´N¬O»ˇ
(C . A) . B
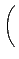

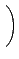 . ło©M
. ło©M
(
C . A)
. B =
C . (
A . B) =
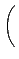


 şˇ¨¬
A . B =
şˇ¨¬
A . B = 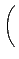

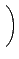 . ¦P˛zĄiŞľ¤ŁĄiŻŕ§ä¨ě
B
. ¦P˛zĄiŞľ¤ŁĄiŻŕ§ä¨ě
B
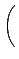

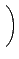 şˇ¨¬
B . A =
şˇ¨¬
B . A = 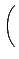

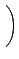 . ©ŇĄH A µ´ąď¤Ł·|¬O M2(R) Şş¤@Ó zero-divisor.
¦]¦ą§Ú̱oĂŇ:
. ©ŇĄH A µ´ąď¤Ł·|¬O M2(R) Şş¤@Ó zero-divisor.
¦]¦ą§Ú̱oĂŇ:
Proposition 5.5.1
Y
R ¬O¤@Ó commutative ring ĄB
A  M2
M2(
R), «h
A ¬O
M2(
R) Şş¤@Ó zero-divisor YĄB°ßY det(
A) = 0
©Î det(
A) ¬O
R Şş¤@Ó zero-divisor.
ĄŃ Proposition 5.5.1 §ÚĚŞľ¦b
M2( ) ©M
M2(
) ©M
M2( ) ¤¤
determinant ¬° 0 ŞşŻx°·|¬O zero-divisor, ¦Ó determinant ¤Ł¬° 0
ŞşŻx°´N¤Ł·|¬O zero-divisor.
) ¤¤
determinant ¬° 0 ŞşŻx°·|¬O zero-divisor, ¦Ó determinant ¤Ł¬° 0
ŞşŻx°´N¤Ł·|¬O zero-divisor.
·í R ¬O commutative ring with 1 ®É M2(R) ·|¦łţ¨Ç unit ©O?
§Ú̦łĄH¤UŞşµ˛ŞG:
Proposition 5.5.2
Y
R ¬O¤@Ó
commutative ring with 1 ĄB
A  M2
M2(
R), «h
A ¬O
M2(
R)
Şş¤@Ó unit YĄB°ßY det(
A) ¬O
R Şş¤@Ó unit.
µý ©ú.
°˛ł]
A ¬O
M2(
R) Şş¤@Ó unit, «h¦s¦b
B  M2
M2(
R) şˇ¨¬
§QĄÎ¦ˇ¤l (
5.3) ±o
det(A) . det(B) = det(B) . det(A) = 1.
µM¦Ó
det(
A), det(
B)
 R
R, ¬G±o det(
A) ¬O
R Şş¤@Ó unit.
¤Ď¤§, Y
A = 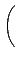
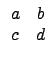
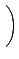 ĄB
det(A) =
ĄB
det(A) =  ¬O R Şş¤@Ó unit, «h¦ŇĽ
¬O R Şş¤@Ó unit, «h¦ŇĽ
¦]
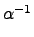
 R
R, §ÚĚŞľ
B  M2
M2(
R). §QĄÎ¦ˇ¤l
(
5.2), Ąi±o
¦]¦ą
A ¬O
M2(
R) Şş¤@Ó unit.

ĄŃ Proposition 5.5.2 Şľ¦b
M2( ) ¤¤±©¦ł determinant ¬O
±1 ŞşŻx°¤ ·|¬O unit, ¦Ó¦b
M2(
) ¤¤±©¦ł determinant ¬O
±1 ŞşŻx°¤ ·|¬O unit, ¦Ó¦b
M2( ) ¤¤©Ň¦ł determinant ¤Ł¬O
0 ŞşŻx°łŁ·|¬O unit.
) ¤¤©Ň¦ł determinant ¤Ł¬O
0 ŞşŻx°łŁ·|¬O unit.



¤U¤@¶: The Hamilton quaternions
¤W¤@¶: ¤@¨Ç Noncommutative Ring
«e¤@¶: ¤@¨Ç Noncommutative Ring
Administrator
2005-06-18
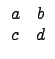
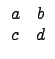
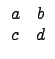
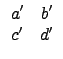
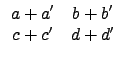
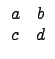
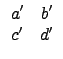
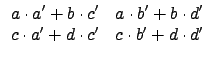

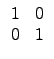
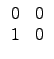
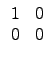
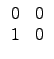
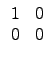
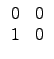
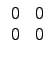
![]()
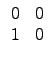
![]() ©M
©M
![]()
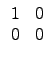
![]() ¬O M2(R) Şş zero-divisor.
¦P®É¦błoӨҤl¸Ě§Ṳ́]µo˛¦b¤@Ó noncommutative ring ¤¤¬O¦łĄiŻŕµoĄÍ
a . b = 0 ¦ý
b . a
¬O M2(R) Şş zero-divisor.
¦P®É¦błoӨҤl¸Ě§Ṳ́]µo˛¦b¤@Ó noncommutative ring ¤¤¬O¦łĄiŻŕµoĄÍ
a . b = 0 ¦ý
b . a![]() 0 Şş˛¶H.
0 Şş˛¶H.
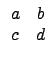
![]()
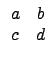
![]()
![]()
![]()

![]() ¦ý det(A) = 0 ®É, ĄŃ©ó
¦ý det(A) = 0 ®É, ĄŃ©ó
![]()
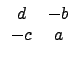
![]()
![]()
![]()

![]() , ĄŃ¦ˇ¤l (5.2) Şľ A ¬O¤@Ó zero-divisor.
, ĄŃ¦ˇ¤l (5.2) Şľ A ¬O¤@Ó zero-divisor.
![]()
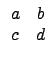
![]()
![]()
![]()

![]() ĄB
det(A) =
ĄB
det(A) = ![]() ¬O R Şş¤@Ó zero-divisor. ł]
¬O R Şş¤@Ó zero-divisor. ł]
![]()
![]() 0 ¬O R ¤¤¤@¤¸ŻŔşˇ¨¬
0 ¬O R ¤¤¤@¤¸ŻŔşˇ¨¬
![]() .
. ![]() = 0.
¦łĄH¤U¨âşŘĄiŻŕµoĄÍ:
= 0.
¦łĄH¤U¨âşŘĄiŻŕµoĄÍ:
![]() ,
b .
,
b . ![]() ,
c .
,
c . ![]() ©M
d .
©M
d . ![]() łŁµĄ©ó 0: ¦ą®ÉĄO
B =
łŁµĄ©ó 0: ¦ą®ÉĄO
B = ![]()
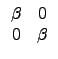
![]() , ¦p¦ą¤@¨Ó¦]
, ¦p¦ą¤@¨Ó¦]
![]()
![]() 0, ©ŇĄH
B
0, ©ŇĄH
B![]()
![]()

![]() , ¦ý¬O
, ¦ý¬O
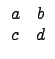
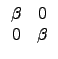
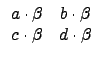
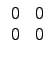
![]() ,
b .
,
b . ![]() ,
c .
,
c . ![]() ©M
d .
©M
d . ![]() ¤ŁĄţ¬° 0:
«h§Ú̦Ҽ
¤ŁĄţ¬° 0:
«h§Ú̦Ҽ
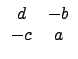
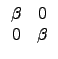
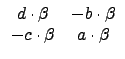
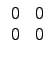
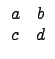
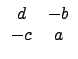
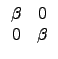
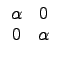
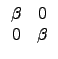
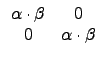
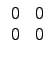
![]()
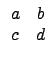
![]() ĄB
det(A) =
ĄB
det(A) = ![]() ¤Ł¬O R Şş zero-divisor ®É¤S·|«çĽË©O? °˛ł]¦s¦b
B =
¤Ł¬O R Şş zero-divisor ®É¤S·|«çĽË©O? °˛ł]¦s¦b
B = ![]()
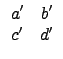
![]()
![]()
![]()

![]() (¤]´N¬O»ˇ a', b', c' ©M d' ¤ŁĄţ¬° 0) şˇ¨¬
A . B =
(¤]´N¬O»ˇ a', b', c' ©M d' ¤ŁĄţ¬° 0) şˇ¨¬
A . B = ![]()

![]() . ¦ą®É¦ŇĽ
C =
. ¦ą®É¦ŇĽ
C = ![]()
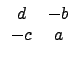
![]() , «hĄŃ¦ˇ¤l (5.2) Şľ
, «hĄŃ¦ˇ¤l (5.2) Şľ
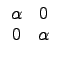
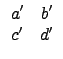
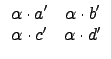

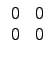




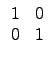
![]()
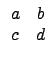
![]() ĄB
det(A) =
ĄB
det(A) = ![]() ¬O R Şş¤@Ó unit, «h¦ŇĽ
¬O R Şş¤@Ó unit, «h¦ŇĽ