


下一頁: 中級 Ring 的性質
上一頁: 一些 Noncommutative Ring
前一頁: Matrix ring M2(R)
大家都知道複數
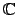 的元素可寫成
a + bi, 其中
a, b
的元素可寫成
a + bi, 其中
a, b 
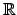 而
i
而
i 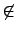
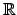 滿足
i2 = - 1. 我們都知道如何定
滿足
i2 = - 1. 我們都知道如何定
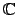 中的加法和乘法, 也就是: 若
a + bi, a' + b'i
中的加法和乘法, 也就是: 若
a + bi, a' + b'i 
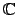 , 則
, 則
(a + bi) + (a' + b'i) = (a + a') + (b + b')i
和
(a + bi) . (a' + b'i) = aa' + ab'i + ba'i + bb'i2 = (aa' - bb') + (ab' + ba')i.
不難驗證在此加法和乘法之下
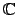 是一個 commutative ring with 1, 其中
0 + 0i 和
1 + 0i
分別是
是一個 commutative ring with 1, 其中
0 + 0i 和
1 + 0i
分別是
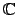 的 0 和 1. 利用大家熟悉的式子
的 0 和 1. 利用大家熟悉的式子
| (a + bi) . (a - bi) = (a2 + b2) + 0i, |
(5.4) |
我們很容易得到若
a + bi 0 + 0i (即 a
0 + 0i (即 a 0 或 b
0 或 b 0), 則
0), 則
(
a +
bi)
. (
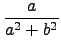
+
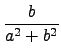 i
i) = 1 + 0
i.
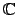 中不等於 0 的數都是 unit, 所以
中不等於 0 的數都是 unit, 所以
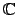 是一個
field.
是一個
field.
利用和由
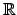 創造出
創造出
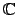 類似的方法, Hamilton 引進了下列的數:
類似的方法, Hamilton 引進了下列的數:
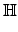
= {
a +
bi +
cj +
dk |
a,
b,
c,
d 
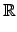
},
其中
i,j,k
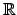 , 我們稱
, 我們稱
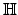 為 the Hamilton quaternions.
我們可以定
為 the Hamilton quaternions.
我們可以定
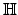 的加法如下: 若
a + bi + cj + dk, a' + b'i + c'j + d'k
的加法如下: 若
a + bi + cj + dk, a' + b'i + c'j + d'k 
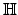 , 則
, 則
(a + bi + cj + dk) + (a' + b'i + c'j + d'k) = (a + a') + (b + b')i + (c + c')j + (d + d')k.
要定義
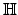 的乘法我們首先定義
i,
j 和
k 間的乘法如下:
的乘法我們首先定義
i,
j 和
k 間的乘法如下:
-
i2 = j2 = k2 = - 1,
-
i . j = k = - j . i,
-
j . k = i = - k . j,
-
k . i = j = - i . k.
對任意的
a + bi + cj + dk, a' + b'i + c'j + d'k 
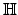 ,
我們定其相乘為一項一項用分配率展隋A將 `實數項' 及
i,j,k
項的係數合併. 也就是說
,
我們定其相乘為一項一項用分配率展隋A將 `實數項' 及
i,j,k
項的係數合併. 也就是說
(
a +
bi +
cj +
dk)
. (
a' +
b'i +
c'j +
d'k) =

+
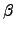 i
i +
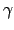 j
j +
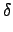 k
k,
 |
= |
aa' - bb' - cc' - dd' |
|
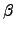 |
= |
ab' + ba' + cd' + dc' |
|
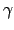 |
= |
ac' - bd' + ca' + db' |
|
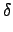 |
= |
ad' + bc' - cb' + da' |
|
不難驗證在此加法和乘法之下
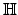 是一個 ring with 1, 其中
0 + 0i + 0j + 0k 和
1 + 0i + 0j + 0k 分別是
是一個 ring with 1, 其中
0 + 0i + 0j + 0k 和
1 + 0i + 0j + 0k 分別是
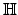 的 0 和 1.
不過
的 0 和 1.
不過
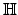 不再是 commutative ring, 這可以由
不再是 commutative ring, 這可以由
(0 + 1i + 0j + 0k) . (0 + 0i + 1j + 0k) = 0 + 0i + 0j + 1k
但
(0 + 0i + 1j + 0k) . (0 + 1i + 0j + 0k) = 0 + 0i + 0j - 1k
看出. 大家很容易就可證出,
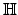 也有類似式子 (5.4)
的重要等式:
也有類似式子 (5.4)
的重要等式:
| (a + bi + cj + dk) . (a - bi - cj - dk) = (a2 + b2 + c2 + d2) + 0i + 0j + 0k. |
(5.5) |
利用式子 (5.5) 我們可以看出, 若
a + bi + cj + dk 0 + 0i + 0j + 0k (即 a, b, c, d 不全為 0), 令
0 + 0i + 0j + 0k (即 a, b, c, d 不全為 0), 令
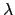 = a2 + b2 + c2 + d2, 則
= a2 + b2 + c2 + d2, 則
(
a +
bi +
cj +
dk)
. (
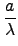
-
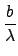 i
i -
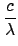 j
j -
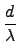 k
k) = 1 + 0
i + 0
j + 0
k.
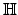 中不等於 0 的數都是 unit,
所以
中不等於 0 的數都是 unit,
所以
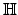 是一個 noncommutative division ring.
是一個 noncommutative division ring.
如果大家不健忘的話, 應該記得
{±1 ±i,±j,±k}
就是我們在 4.7 節介紹的 quaternion group Q8.
事實上對任意的 group 你都可以用類似的方法建構出一個 ring, 這樣的
ring 我們稱為 group ring.



下一頁: 中級 Ring 的性質
上一頁: 一些 Noncommutative Ring
前一頁: Matrix ring M2(R)
Administrator
2005-06-18
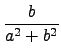 i) = 1 + 0i.
i) = 1 + 0i.
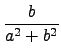 i) = 1 + 0i.
i) = 1 + 0i.
![]() 創造出
創造出
![]() 類似的方法, Hamilton 引進了下列的數:
類似的方法, Hamilton 引進了下列的數: