�U�@��: �s�y��h�� subgroups �W�@��: �� Group ��ʽ� �e�@��: Subgroup

�@�ǯS�� subgroup

�e��Χڭ̧Ʊ�Q�Τ@�� group �� subgroup ��ڭ̤F�ѳo�@�� group. ��w�@�� group ��F trivial subgroup �~�쩳�n��˧��L�� subgroup �O?��M�F�� group �O�S�� nontrivial proper subgroup ��(�H��ڭ̷|��), �b�o�@�`�ڭ̧Ʊ椶�Ф@�ǥi�� nontrivial proper subgroup ��k.

�� G �O�@�� group ��w a $\in$ G, �ڭ̧Ʊ�� a �Ӳ��ͤ@�� subgroup. �ܦ۵M��ڭ̪��D a², a³,..., aⁿ,... ��n�b�o�� subgroup ��, �٦� a^-1, (a²)^-1,...,(aⁿ)^-1,... �]�n�b�䤤, �̫�O�ѤF e �]�n�b�̭�. �� Corollary 1.2.5, �ڭ̪� (aⁿ)^-1 = (a^-1)ⁿ, �ҥH�ڭ̫ܦ۵M��|�w�q�H�U��X:

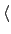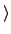
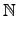
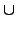
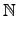
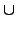
$\displaystyle \langle$ a $\displaystyle \rangle$ : = {aⁿ | n $\displaystyle \in$ $\displaystyle \mathbb {N}$ } $\displaystyle \cup$ {(a^-1)^m | m $\displaystyle \in$ $\displaystyle \mathbb {N}$ } $\displaystyle \cup$ {e}.

�ܮe�� Lemma 1.3.3 (�� Lemma 1.3.4) ��D $\langle$ a $\rangle$ �|�O G ��@�� subgroup. �ڭ̺� $\langle$ a $\rangle$ �� the cyclic subgroup of G generated by a. ��M�F, �p�G�ڭ̿�� a = e �h $\langle$ a $\rangle$ = {e} �o�@�� trivial subgroup. �t�@�譱�p�G�ڭ̥i�H��@�� a �ϱo $\langle$ a $\rangle$ = G, ��ڭ̴N�� G ��@�� cyclic group. �n�`�N��O�ä��O�Ҧ�� group G ��i�H�� a $\in$ G �ϱo $\langle$ a $\rangle$ = G.

Example 1.4.1 �ڭ̵��@�Ӧ��ǦP�Ƿ|�d�V��Ҥl. �|�d�V��]�O�e��L, ��F²�K��]��ڭ̳�� u^.�v �Ӫ�� group ��B��, �ҥH a² = a^.a �� a �M a �B��⦸, a³ ��ܹB��T��... �̦��. �{�b�ڭ̦Ҽ{ $\mathbb {Z}$ �H�[�k�Φ�� group. �� $\langle$ 2 $\rangle$ ��ӬO��˪� subgroup �O? ��ӬO�� 2, 4 = 2 + 2, 6 = 2 + 2 + 2, ...(�d�U�O�d��, ��O�� 2, 4 = 2², 8 = 2³,...) �H�� -2, -4, -6, ... ��Ҳզ�. ��y�ܻ��b�� group ��H 2 �ҧΦ�� cyclic subgroup �Y�O�ѩҦ��ƩҲզ��. �t�~�j�a�ܮe��ݥX�� -2 �]�i��ͦP�˪� subgroup. �j�a�]�i�ܮe��ݥX 1 �Ҳ��ͪ� cyclic subgroup �N�O $\mathbb {Z}$ ��ҥH�ڭ̪��D $\mathbb {Z}$ �ҧΦ��[�k�s�O�@�� cyclic group.

�j�a��ӳ��ٰO�o, �b�@�몺 group ��, a^.b ��o�� b^.a. ��L�] a^.e = e^.a = a �ҥH identity �`�O�M�Ҧ��i�洫��. �ܩ󵹩w�@��, ��Ǥ��i�H�M��洫�O�@�ӫܦ��쪺��D. ��w a $\in$ G, �ڭ̥i�H�Ҽ{

C(a) = {g $\displaystyle \in$ G | g^.a = a^.g}.

�o�Ӷ��X�N�O�j�� G ��i�H�M a �洫��. �ڭ̺٤�� the centralizer of a. ��w��N�� a $\in$ G, �ƹ�W C(a) �|�O G ��@�� subgroup. �Ҧp the centralizer of identity C(e) �N�O G ��.

Proposition 1.4.2 �Y G �O�@�� group �B a $\in$ G, �h C(a) �O G ��@�� subgroup.

�� . �� Lemma 1.3.3, �ڭ̭n�ҩ�: �Y g₁, g₂ $\in$ C(a) �h g₁^.g₂ $\in$ C(a) �٦� g₁^-1 $\in$ C(a). �ƹ�W g₁, g₂ $\in$ C(a) �i�D�ڭ� g₁^.a = a^.g₁ �� g₂^.a = a^.g₂. �]��

(g₁^.g₂)^.a = g₁^.(g₂^.a) = g₁^.(a^.g₂) = (g₁^.a)^.g₂ = (a^.g₁)^.g₂ = a^.(g₁^.g₂).

�]�N�O�� g₁^.g₂ $\in$ C(a). �t�@�譱, �ѩ� g₁^.a = a^.g₁, �U��W g₁^-1 �b��䵥��k��. �ڭ̱o�� (g₁^.a)^.g₁^-1 = a. �A��H g₁^-1 ��䵥��. �ڭ̱o a^.g₁^-1 = g₁^{-1 .}a. �]�N�O�� g₁^-1 $\in$ C(a). $\qedsymbol$

�t�~�@�ر`�� subgroup �O�Ҽ{

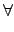Z(G) = {g $\displaystyle \in$ G | g^.x = x^.g, $\displaystyle \forall$ x $\displaystyle \in$ G}.

�ڭ̤@�� Z(G) �� G �� center. �`�N C(a) �O�M G ��S�w�� a �i�洫��Ҧ��X, �� Z(G) �O�M G ��Ҧ��i�洫��Ҧ��X. �ҥH�ڭ̫ܮe��i�ұo

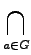Z(G) = $\displaystyle \bigcap_{a\in G}^{}$ C(a).

��ҩ� C(a) �O G �� subgroup ��k�ڭ̤]�i�H�ҩ� Z(G) �]�O G �� subgroup. �b�o�̧ڭ̤��A��ҩ��L��@�U�ڭ̱N�|�Υt�@�جݪk�ӻ�� Z(G) �O G �� subgroup.

�U�@��: �s�y��h�� subgroups �W�@��: �� Group ��ʽ� �e�@��: Subgroup

Administrator 2005-06-18

�@�ǯS���� subgroup

�@�ǯS�� subgroup